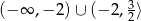Zadanie nr 1322775
Wyznacz dziedzinę funkcji 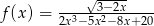 .
.
Rozwiązanie
Ze względu na pierwiastek w liczniku musi być
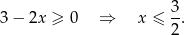
Musimy z tego zbioru wyrzucić jeszcze miejsca zerowe mianownika.
Sposób I
Rozkładamy wielomian w mianowniku grupując wyrazy.
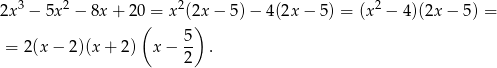
Zatem miejscami zerowymi mianownika są liczby 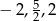 i dziedziną funkcji jest zbiór
i dziedziną funkcji jest zbiór
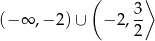
Sposób II
Sprawdzając dzielniki wyrazu wolnego łatwo znaleźć pierwiastek 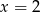 . Dzielimy ten wielomian przez
. Dzielimy ten wielomian przez 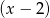 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
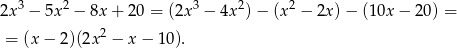
Dalej 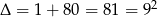 ,
, 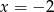 lub
lub 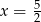 . Zatem miejsca zerowe mianownika to liczby
. Zatem miejsca zerowe mianownika to liczby 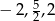 i dziedziną funkcji
i dziedziną funkcji  jest zbiór
jest zbiór 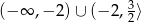 .
.
Odpowiedź: