/Szkoła podstawowa/Liczby/Operacje na cyfrach

Zadanie nr 3239205

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że różnica każdych dwóch liczb trzycyfrowych, napisanych za pomocą tych samych cyfr, jest podzielna przez 3.

Rozwiązanie

Sposób I

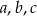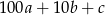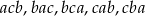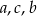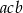Jeżeli cyfry liczby trzycyfrowej są równe a,b,c (czyli jest ona równa 10 0a+ 10b+ c ), to jest 5 innych liczb, które można utworzyć z tych samych cyfr: acb,bac,bca,cab,cba (dla prostoty będziemy zapisywać liczbę o kolejnych cyfrach a,c,b jako acb , oczywiście nie ma to nic wspólnego z iloczynem 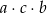a⋅c ⋅b ). W każdym z przypadków liczymy różnicę

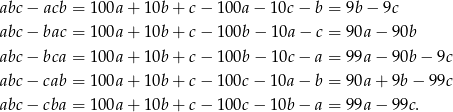
abc − acb = 1 00a+ 10b + c− 100a − 10c − b = 9b − 9c abc − bac = 1 00a+ 10b + c− 100b − 10a − c = 9 0a− 90b abc − bca = 1 00a+ 10b + c− 100b − 10c − a = 9 9a− 90b− 9c abc − cab = 1 00a+ 10b + c− 100c − 10a − b = 9 0a+ 9b− 99c abc − cba = 1 00a+ 10b + c− 100c − 10b − a = 9 9a− 99c.

Oczywiście każda z otrzymanych liczb dzieli się przez 9.

Gdy się chwilę zastanowić, to powinno być jasne, że analogiczna własność zachodzi bez względu na ilość cyfr wyjściowej liczby. Wynika to z tego, że odejmując od siebie dwie liczby o takich samych cyfrach, ale zapisanych w innej kolejności, otrzymujemy w wyniku sumę wyrażeń postaci 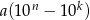a(10n − 10k) , gdzie a jest cyfrą wyjściowej liczby. Pozostaje teraz zauważyć, że liczba 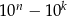10n − 10k jest zawsze podzielna przez 9.

Sposób II

Zamiast się męczyć z rachunkami, możemy skorzystać z faktu, że liczba daje przy dzieleniu przez 3 taką samą resztę jak suma jej cyfr (jest to lekkie uogólnienie cechy podzielności przez 3). Jeżeli w liczbie zmienimy kolejność cyfr, to suma cyfr się nie zmieni, więc otrzymana liczba daje taką samą resztę z dzielenia przez 3 jak liczba wyjściowa. Zatem ich różnica dzieli się przez 3.

Wersja PDF