Zestaw użytkownika nr 5012_3478
Próba przed maturą 2011poziom rozszerzonyCzas pracy: 180 min.
Liczby 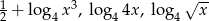 w podanej kolejności, dla pewnej rzeczywistej wartości
w podanej kolejności, dla pewnej rzeczywistej wartości  , są trzema kolejnymi początkowymi wyrazami nieskończonego ciągu arytmetycznego. Wyznacz
, są trzema kolejnymi początkowymi wyrazami nieskończonego ciągu arytmetycznego. Wyznacz  oraz sumę czterdziestu początkowych wyrazów tego ciągu.
oraz sumę czterdziestu początkowych wyrazów tego ciągu.
Wyznacz wszystkie wartości parametru 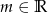 , dla których równanie
, dla których równanie 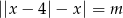 ma tylko jedno rozwiązanie.
ma tylko jedno rozwiązanie.
W trapez 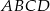 , gdzie
, gdzie 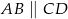 i
i 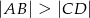 , wpisano okrąg (patrz rysunek).
, wpisano okrąg (patrz rysunek).
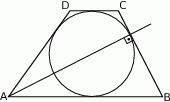
Dwusieczna kąta ostrego przy wierzchołku 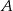 jest prostopadła do ramienia
jest prostopadła do ramienia 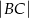 .
.
- Wykaż, że dwusieczna kąta przy wierzchołku
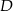 jest równoległa do ramienia
jest równoległa do ramienia 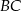 .
. - Oblicz
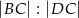 .
.
Z półokręgów budujemy krzywą (patrz rysunek). Pierwszy półokrąg ma promień długości 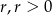 , a promień każdego następnego półokręgu stanowi
, a promień każdego następnego półokręgu stanowi  promienia poprzedniego. Niech
promienia poprzedniego. Niech  oznacza liczbę półokręgów tworzących tę krzywą. Udowodnij, że dla dowolnej liczby naturalnej dodatniej
oznacza liczbę półokręgów tworzących tę krzywą. Udowodnij, że dla dowolnej liczby naturalnej dodatniej  długość krzywej jest mniejsza od
długość krzywej jest mniejsza od 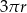 .
.

Punkty przecięcia paraboli 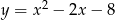 z prostą
z prostą 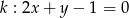 są końcami przekątnej rombu, którego pole jest równe 30. Oblicz współrzędne wierzchołków tego rombu.
są końcami przekątnej rombu, którego pole jest równe 30. Oblicz współrzędne wierzchołków tego rombu.
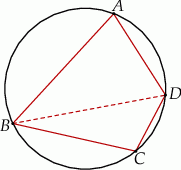
Czworokąt 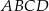 jest wpisany w okrąg o promieniu
jest wpisany w okrąg o promieniu 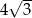 (patrz rysunek). Przekątna
(patrz rysunek). Przekątna 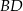 czworokąta ma długość 12. Iloczyn sinusów wszystkich kątów wewnętrznych czworokąta jest równy
czworokąta ma długość 12. Iloczyn sinusów wszystkich kątów wewnętrznych czworokąta jest równy 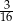 . Wiedząc, że
. Wiedząc, że 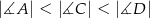 , oblicz miary kątów czworokąta
, oblicz miary kątów czworokąta 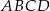 .
.
W wyniku podzielenia wielomianu 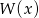 przez
przez 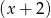 otrzymujemy iloraz
otrzymujemy iloraz 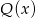 i resztę 0. Jeśli natomiast podzielimy wielomian
i resztę 0. Jeśli natomiast podzielimy wielomian 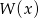 przez
przez 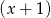 , to otrzymamy iloraz
, to otrzymamy iloraz 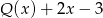 i resztę 2.
i resztę 2.
- Wyznacz wielomian
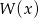 .
. - Rozwiąż nierówność
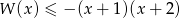 .
.
Ze zbioru 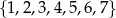 losujemy kolejno, bez zwracania trzy cyfry i tworzymy liczbę trzycyfrową: pierwsza wylosowana cyfra jest cyfrą setek, druga – cyfrą dziesiątek, a trzecia – cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że otrzymana liczba ma następującą własność: różnica między największą i najmniejszą cyfrą tej liczby jest nie większa niż 3.
losujemy kolejno, bez zwracania trzy cyfry i tworzymy liczbę trzycyfrową: pierwsza wylosowana cyfra jest cyfrą setek, druga – cyfrą dziesiątek, a trzecia – cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że otrzymana liczba ma następującą własność: różnica między największą i najmniejszą cyfrą tej liczby jest nie większa niż 3.
Dane jest równanie kwadratowe 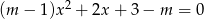 z niewiadomą
z niewiadomą  i parametrem
i parametrem 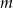 .
.
- Znajdź wzór i dziedzinę funkcji
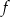 , która zmiennej rzeczywistej
, która zmiennej rzeczywistej 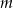 przyporządkowuje iloczyn dwóch różnych pierwiastków danego równania. Naszkicuj wykres funkcji
przyporządkowuje iloczyn dwóch różnych pierwiastków danego równania. Naszkicuj wykres funkcji 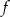 w prostokątnym układzie współrzędnych.
w prostokątnym układzie współrzędnych. - Wykaż, że do wykresu funkcji
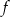 należą tylko trzy punkty o obu współrzędnych całkowitych.
należą tylko trzy punkty o obu współrzędnych całkowitych.
Podstawą ostrosłupa 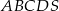 jest kwadrat
jest kwadrat 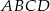 (patrz rysunek).
(patrz rysunek).
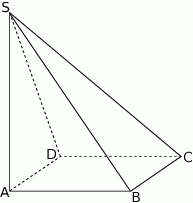
Krawędź 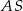 jest wysokością tego ostrosłupa. Odległość punktu
jest wysokością tego ostrosłupa. Odległość punktu 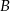 od krawędzi
od krawędzi 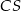 jest równa
jest równa 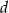 , a kąt dwuścienny między ścianami
, a kąt dwuścienny między ścianami 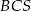 i
i 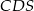 ma miarę
ma miarę 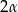 , gdzie
, gdzie 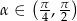 . Oblicz:
. Oblicz:
- odległość punktu
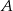 od krawędzi
od krawędzi 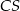
- wysokość tego ostrosłupa.

