Zestaw użytkownika nr 5682_5040
SprawdzianFunkcje kwadratowe20 Stycznia 2011Czas pracy: 45 min.
Liczby 7 i -3 są pierwiastkami równania
A) 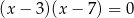
B) 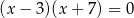
C) 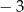
D) 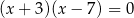
Mniejszą z dwóch liczb spełniających równanie 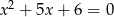 jest
jest
A) -1 B) -3 C) -6 D) -2
Równanie 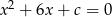 nie ma rozwiązania, gdy
nie ma rozwiązania, gdy
A) 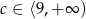 B)
B) 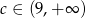 C)
C) 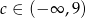 D)
D) 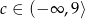
Zbiorem rozwiązań nierówności 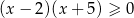 jest
jest
A) 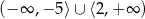
B) 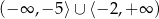
C) 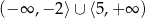
D) 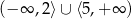
Liczb pierwszych należących do przedziału będącego rozwiązaniem nierówności 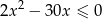 jest
jest
A) 5 B) 6 C) nieskończenie wiele D) 7
Największą wartością funkcji kwadratowej 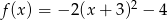 jest
jest
A) 3 B) -2 C) -4 D) 4
Funkcja 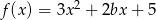 maleje w przedziale
maleje w przedziale 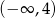 i rośnie w przedziale
i rośnie w przedziale 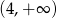 . Wynika stąd, że
. Wynika stąd, że
A) 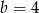 B)
B) 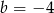 C)
C) 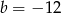 D)
D) 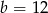
Funkcja 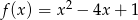 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 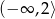 B)
B) 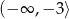 C)
C) 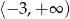 D)
D) 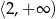
Na rysunku obok
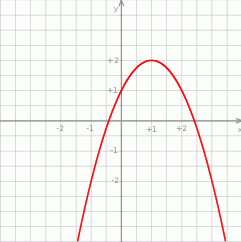
przedstawiony jest wykres funkcji o wzorze
A) 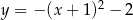 B)
B) 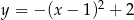 C)
C) 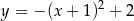 D)
D) 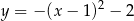
Gdy przesuniemy wykres funkcji 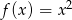 o 7 jednostek w lewo i 4 jednostki w dół, to otrzymamy wykres funkcji
o 7 jednostek w lewo i 4 jednostki w dół, to otrzymamy wykres funkcji
A) 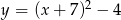 B)
B) 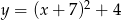 C)
C) 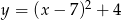 D)
D)