/Szkoła średnia/Funkcje/Logarytm/Dziedzina

Zadanie nr 6260457

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz dziedzinę funkcji

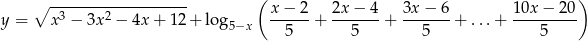
∘ ------------------- ( x− 2 2x − 4 3x − 6 10x − 20 ) y = x3 − 3x2 − 4x + 12 + lo g5−x -----+ -------+ -------+ ...+ --------- 5 5 5 5

Rozwiązanie

Sprawdźmy najpierw kiedy wyrażenie pod pierwiastkiem jest nieujemne. W tym celu szukamy pierwiastków występującego tam wielomianu. Łatwo odgadnąć pierwiastek 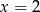x = 2 . Dzielimy ten wielomian przez 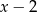x − 2 . My zrobimy to grupując wyrazy.

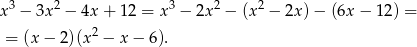
x 3 − 3x 2 − 4x+ 12 = x3 − 2x 2 − (x 2 − 2x )− (6x− 12) = 2 = (x− 2)(x − x− 6).

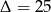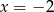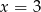Rozkładamy jeszcze trójmian kwadratowy. Δ = 2 5 , x = − 2 lub x = 3 . Mamy zatem nierówność

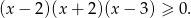
(x− 2)(x + 2)(x − 3) ≥ 0 .

Jej rozwiązaniem (np. z metody węża) jest zbiór

x ∈ ⟨− 2,2⟩∪ ⟨3,∞ ).

PIC

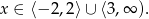
Zajmijmy się teraz logarytmem. Podstawa musi być dodatnia i różna od 1, czyli

x ∈ (− ∞ ,4)∪ (4 ,5 ).

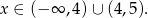
Wyrażenie pod logarytmem jest sumą 10 wyrazów ciągu arytmetycznego o różnicy 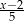x−2- 5 . Suma ta jest więc równa

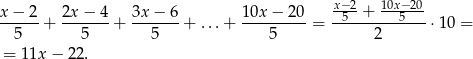
x− 2 2x − 4 3x − 6 10x − 20 x−-2+ 10x−-20 ------+ -------+ -------+ ...+ ---------= -5-------5---⋅ 10 = 5 5 5 5 2 = 11x − 22.

Zatem

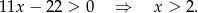
11x − 22 > 0 ⇒ x > 2.

Z trzech otrzymanych warunków mamy dziedzinę (wszystkie trzy muszą zachodzić na raz).

⟨3,4) ∪ (4,5).

 
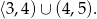
Odpowiedź: ⟨3,4) ∪ (4,5)

Wersja PDF