/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Równania z pierwiastkami

Zadanie nr 7062698

Dodaj do ulubionych
Dodaj do rozwiązanych

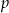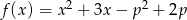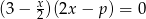Dla jakiego parametru p iloczyn miejsc zerowych funkcji 2 2 f(x) = x + 3x− p + 2p jest równy mniejszemu pierwiastkowi równania (3 − x2)(2x − p) = 0 .

Rozwiązanie

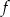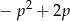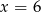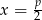Na mocy wzorów Viète’a, iloczyn miejsc zerowych f (jeżeli istnieją! – na to trzeba uważać) jest równy − p 2 + 2p . Podane równanie ma dwa rozwiązania x = 6 i x = p2 . W zależności od tego, które z nich jest mniejsze mamy dwa przypadki.

Jeżeli 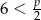p 6 < 2 , czyli 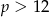p > 12 , to mamy równanie

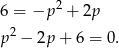
6 = −p 2 + 2p p2 − 2p + 6 = 0 .

Równanie to nie ma rozwiązań (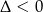Δ < 0 ).

Jeżeli 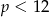p < 12 , to mamy równanie

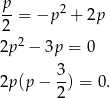
p-= −p 2 + 2p 2 2p 2 − 3p = 0 2p (p − 3-) = 0. 2

Łatwo sprawdzić, że dla obu wartości 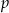p funkcja 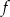f ma pierwiastki.  
Odpowiedź: 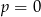p = 0 lub p = 3 2

Wersja PDF