Zestaw użytkownika nr 7287_4655

FUNKCJA LOGARYTMICZNAMATURA ROZSZERZONA2012Czas pracy: 180 min.

Zadanie 1

Wyznacz wszystkie wartości parametru 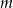, dla których dziedziną funkcji

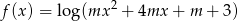
2 f(x) = log (mx + 4mx + m + 3)

jest zbiór wszystkich liczb rzeczywistych.

Zadanie 2

Wyznacz wszystkie wartości parametru 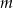, dla których dziedziną funkcji

2 2 f(x ) = log[(m + m − 6)x + (m − 2)x + 1]

jest zbiór wszystkich liczb rzeczywistych.

Zadanie 3

Wyznacz dziedzinę funkcji 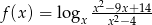x2−-9x+14- f(x ) = lo gx x2− 4 .

Zadanie 4

Wyznacz dziedzinę funkcji 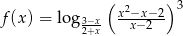( 2 )3 f(x ) = lo g3−x x-−xx−−2-2 2+x

Zadanie 5

Dany jest wielomian 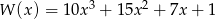3 2 W (x) = 10x + 15x + 7x + 1 .

Zapisz wielomian 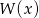jako iloczyn wielomianów liniowych.
Określ dziedzinę funkcji .

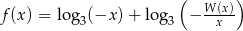Zadanie 6

Funkcja 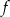dana jest wzorem

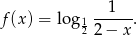
1 f(x) = log 1------. 22 − x

Określ dziedzinę funkcji 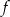i naszkicuj jej wykres w przedziale ⟨− 6,0⟩ .

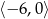Zadanie 7

Dana jest funkcja 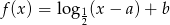f(x ) = lo g12(x − a) + b . Wyznacz wartości parametrów i 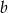, jeśli wiesz, że dziedziną funkcji jest przedział 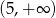(5,+ ∞ ) i do wykresu należy punkt 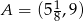A = (51,9) 8 . Podaj wzór tej funkcji.

Zadanie 8

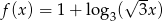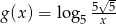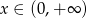Naszkicuj wykresy funkcji √ -- f(x) = 1 + log 3( 3x ) i 5√-5 g(x) = log 5 x , gdzie x ∈ (0,+ ∞ ) . Odczytaj z wykresów zbiór rozwiązań nierówności f (x) ≤ g(x) .

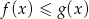Zadanie 9

Dana jest funkcja 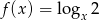f(x ) = lo gx2 .

Określ dziedzinę funkcji .
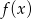Naszkicuj wykres funkcji .
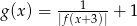Odczytaj z wykresu maksymalne przedziały monotoniczności funkcji .

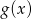Arkusz Wersja PDF