Zadanie nr 7911089
Sinus pewnego kąta ostrego  , liczba
, liczba  oraz cosinus tego samego kąta
oraz cosinus tego samego kąta  tworzą w podanej kolejności ciąg geometryczny. Oblicz sumę
tworzą w podanej kolejności ciąg geometryczny. Oblicz sumę 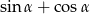 .
.
Rozwiązanie
Jeżeli trzy liczby 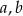 i
i  tworzą ciąg geometryczny to
tworzą ciąg geometryczny to 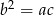 .
.
Sposób I
Mamy równość
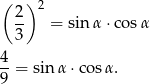
Korzystamy teraz z tożsamości
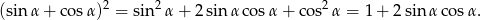
Ponieważ  jest kątem ostrym mamy
jest kątem ostrym mamy
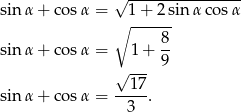
Sposób II
Będziemy korzystać ze wzorów
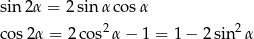
Mamy równanie
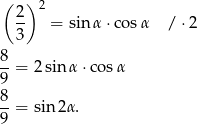
Dalszy plan działania jest następujący, z jedynki trygonometrycznej wyliczymy 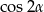 a ze wzorów na
a ze wzorów na 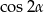 wyliczymy
wyliczymy 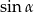 i
i 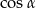 . Liczymy
. Liczymy
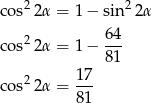
Mamy zatem 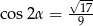 lub
lub 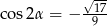 (pomimo, że
(pomimo, że  jest kątem ostrym,
jest kątem ostrym, 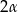 już taki być nie musi, nie wiemy więc czy cosinus jest dodatni). Mamy wtedy odpowiednio
już taki być nie musi, nie wiemy więc czy cosinus jest dodatni). Mamy wtedy odpowiednio
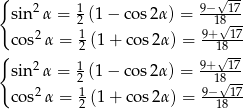
W każdym z przypadków
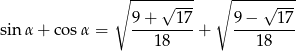
No i mamy ciekawe ćwiczenie, żeby sprawdzić, że ten wynik pokrywa się z tym co uzyskaliśmy poprzednio.
Sposób III
Oznaczmy 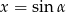 . Wtedy
. Wtedy 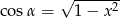 . Mamy równanie
. Mamy równanie
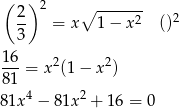
Jest to zwykłe równanie dwukwadratowe, podstawiamy 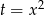 i mamy
i mamy 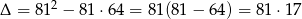 , skąd
, skąd
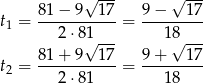
Każdy z przypadków prowadzi do takiego samego wyniku jak w sposobie II.
Odpowiedź: