Zadanie nr 6009387
Drut o długości 72 cm rozcięto na dwa kawałki i z każdego kawałka zbudowano brzeg trójkąta równoramiennego, przy czym stosunek długości ramienia do długości podstawy w jednym trójkącie wynosi 5:8, a w drugim 13:10. Jakie obwody mają te trójkąty jeżeli suma ich pól jest najmniejsza z możliwych?
Rozwiązanie
Oznaczmy długości ramion otrzymanych trójkątów przez  i
i 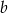 odpowiednio.
odpowiednio.
Z podanych informacji, podstawy tych trójkątów mają długości 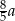 i
i 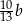 odpowiednio. Wiemy zatem, że
odpowiednio. Wiemy zatem, że
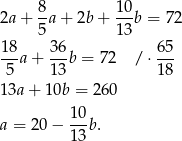
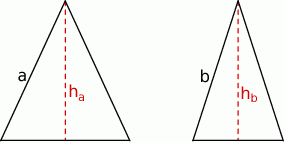
Aby obliczyć pola otrzymanych trójkątów prostokątnych, liczymy ich wysokości z twierdzenia Pitagorasa (inny sposób, to zastosowanie wzoru Herona).
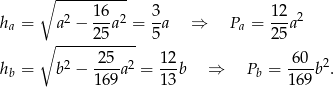
Musimy zatem znaleźć wartość 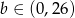 (bo
(bo 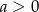 ), dla której funkcja
), dla której funkcja
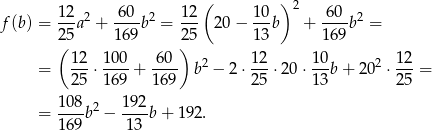
przyjmuje najmniejszą wartość. Ponieważ wykresem tej funkcji jest parabola o ramionach skierowanych do góry, wartość najmniejszą przyjmuje ona w wierzchołku, czyli w punkcie
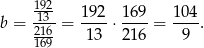
Cały obwód trójkąta o ramieniu 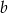 jest więc równy
jest więc równy
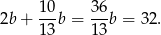
Trójkąt o ramieniu  ma więc obwód
ma więc obwód 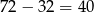 .
.
Odpowiedź: 40 cm i 32 cm

