/Szkoła średnia/Zadania maturalne/Matura 2020/Matura próbna
Lubelska próba przed maturą
z matematyki (dla klas drugich)
poziom podstawowy grupa I 14 maja 2019 Czas pracy: 170 minut
Zadania zamknięte
Wartość wyrażenia 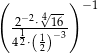 jest równa
jest równa
A) 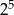 B)
B) 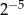 C)
C) 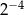 D)
D) 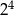
Różnica liczby  i jej kwadratu jest największa dla liczby
i jej kwadratu jest największa dla liczby  równej
równej
A) 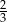 B)
B) 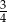 C)
C) 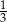 D)
D) 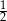
Iloczyn liczby 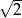 i odwrotności liczby
i odwrotności liczby 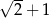 jest równy
jest równy
A) 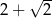 B)
B) 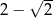 C)
C) 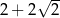 D)
D) 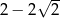
Cenę roweru obniżono o 20%, a po miesiącu podniesiono o 10%. W wyniku obu operacji finansowych cena roweru zmniejszyła się o
A) 10% B) 11% C) 12% D) 15%
Wartość liczbowa wyrażenia 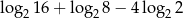 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Jeśli miejscem zerowym funkcji 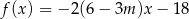 jest liczba 3, to wynika stąd, że
jest liczba 3, to wynika stąd, że
A) 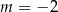 B)
B) 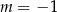 C)
C) 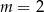 D)
D) 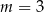
Jeżeli 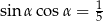 , wartość liczbowa wyrażenia
, wartość liczbowa wyrażenia 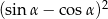 jest równa
jest równa
A)  B)
B)  C)
C)  D) 1
D) 1
Dana jest prosta 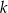 o równaniu
o równaniu 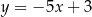 . Równanie prostej prostopadłej do prostej
. Równanie prostej prostopadłej do prostej 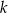 i przechodzącej przez punkt
i przechodzącej przez punkt 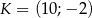 ma postać
ma postać
A) 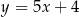 B)
B) 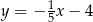 C)
C) 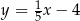 D)
D) 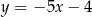
Cięciwa okręgu ma długość 16 cm i jest oddalona od jego środka o 2 cm. Promień tego okręgu ma długość
A) 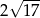 B)
B) 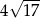 C)
C) 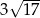 D)
D) 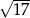
Dziedziną funkcji określonej wzorem 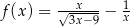 jest
jest
A) 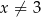 B)
B) 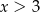 C)
C) 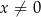 D)
D) 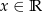
Miara kąta wpisanego opartego na  długości okręgu jest równa
długości okręgu jest równa
A) 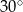 B)
B) 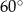 C)
C) 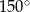 D)
D) 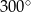
Rozwiązaniem równania 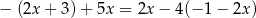 jest liczba
jest liczba
A) 1 B) 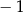 C) 2 D)
C) 2 D) 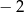
Zbiorem rozwiązań nierówności liniowej 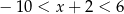 jest przedział liczbowy
jest przedział liczbowy
A) 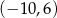 B)
B) 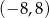 C)
C) 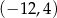 D)
D) 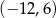
Punkty 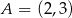 i
i 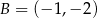 są sąsiednimi wierzchołkami kwadratu
są sąsiednimi wierzchołkami kwadratu 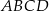 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 36 B) 30 C) 32 D) 34
Jeśli 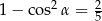 i
i  jest kątem ostrym, to
jest kątem ostrym, to 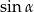 jest równy
jest równy
A) 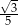 B)
B) 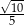 C)
C)  D)
D) 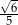
Jeśli 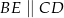 oraz
oraz 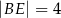 ,
, 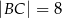 i
i 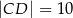 (patrz rysunek),
(patrz rysunek),
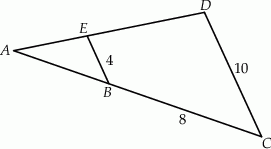
to długość odcinka 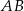 jest równa
jest równa
A) 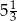 B)
B) 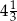 C)
C) 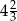 D)
D) 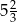
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 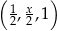 . Wówczas
. Wówczas
A) 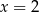 B)
B) 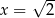 C)
C) 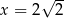 D)
D) 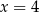
Punkt 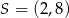 jest środkiem odcinka
jest środkiem odcinka 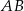 , gdzie
, gdzie 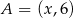 i
i 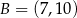 dla
dla  równego
równego
A) 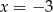 B)
B) 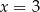 C)
C) 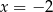 D)
D) 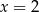
Jeżeli 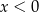 , to wartość wyrażenia
, to wartość wyrażenia 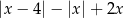 jest równa
jest równa
A) 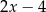 B)
B) 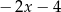 C)
C) 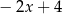 D)
D) 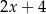
Dany jest ciąg arytmetyczny 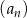 , w którym różnica
, w którym różnica 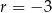 oraz
oraz 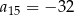 . Wówczas pierwszy wyraz tego ciągu jest równy
. Wówczas pierwszy wyraz tego ciągu jest równy
A) 8 B) 10 C) 12 D) 14
Suma wszystkich wyrazów ciągu arytmetycznego, w którym 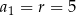 , a ostatni wyraz wynosi 250 jest równa
, a ostatni wyraz wynosi 250 jest równa
A) 6385 B) 6475 C) 6375 D) 6575
Jeżeli wiadomo, że punkty 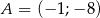 i
i 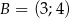 należą do wykresu funkcji liniowej, to ta funkcja opisana jest wzorem
należą do wykresu funkcji liniowej, to ta funkcja opisana jest wzorem
A) 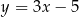 B)
B) 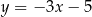 C)
C) 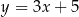 D)
D) 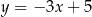
Kąt  na rysunku obok ma miarę
na rysunku obok ma miarę
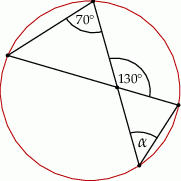
A) 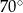 B)
B) 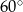 C)
C) 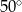 D)
D) 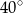
Aby otrzymać wykres funkcji 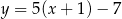 , należało wykres funkcji
, należało wykres funkcji 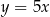 przesunąć A) o 1 jednostkę w lewo i 7 ku dołowi B) o 1 jednostkę w prawo i 7 ku górze
przesunąć A) o 1 jednostkę w lewo i 7 ku dołowi B) o 1 jednostkę w prawo i 7 ku górze
C) o 1 jednostkę w prawo i 7 ku dołowi D) o 1 jednostkę w lewo i 7 ku górze
Funkcja kwadratowa określona jest wzorem 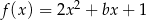 . Jeżeli
. Jeżeli 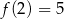 , to
, to
A) 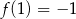 B)
B) 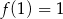 C)
C) 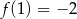 D)
D) 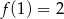
Zadania otwarte
Rozwiąż nierówność 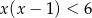 .
.
Wyznacz odległość punktu 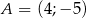 od miejsca zerowego funkcji
od miejsca zerowego funkcji 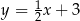 .
.
Liczby 1 i 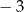 są miejscami zerowymi funkcji kwadratowej
są miejscami zerowymi funkcji kwadratowej 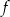 oraz do jej wykresu należy punkt
oraz do jej wykresu należy punkt 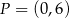 . Wyznacz wzór ogólny tej funkcji.
. Wyznacz wzór ogólny tej funkcji.
Wykaż, że ciąg liczbowy o wyrazie ogólnym 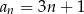 , gdzie
, gdzie 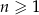 , jest ciągiem arytmetycznym.
, jest ciągiem arytmetycznym.
Matka i córka mają łącznie 68 lat, a 8 lat temu matka był trzykrotnie starsza od córki. Ile lat ma matka, a ile córka?
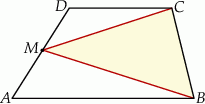
Punkt 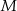 jest środkiem boku
jest środkiem boku 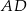 . Udowodnij, że pole trójkąta
. Udowodnij, że pole trójkąta 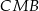 jest połową pola trapezu
jest połową pola trapezu 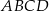 (
( ).
).
Dana jest funkcja kwadratowa określona wzorem 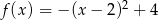 .
.
- podaj współrzędne wierzchołka paraboli będącej wykresem tej funkcji.
- podaj zbiór wartości tej funkcji.
- podaj równanie osi symetrii paraboli będącej wykresem tej funkcji.
- podaj wzór tej funkcji w postaci ogólnej.
W okręgu o promieniu 8 cm poprowadzono cięciwę 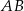 . Długość łuku
. Długość łuku 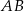 jest równa
jest równa 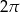 . Oblicz miarę kąta ostrego zawartego między cięciwą
. Oblicz miarę kąta ostrego zawartego między cięciwą 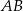 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 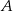 .
.
Pierwszy wyraz ciągu arytmetycznego 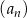 jest równy 4, a suma sześciu początkowych wyrazów tego ciągu wynosi 84.
jest równy 4, a suma sześciu początkowych wyrazów tego ciągu wynosi 84.
- Oblicz sumę pięćdziesięciu początkowych wyrazów tego ciągu.
- Dla jakiego
 liczby
liczby 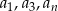 tworzą ciąg geometryczny?
tworzą ciąg geometryczny?

