/Szkoła średnia/Zadania maturalne/Matura 2023
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom podstawowy 2 czerwca 2023 Czas pracy: 180 minut
Wszystkich liczb całkowitych dodatnich spełniających nierówność 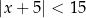 jest
jest
A) 9 B) 10 C) 20 D) 21
Dla każdej dodatniej liczby rzeczywistej  iloczyn
iloczyn 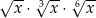 jest równy
jest równy
A)  B)
B) 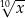 C)
C) 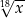 D)
D) 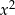
Wykaż, że dla każdej liczby całkowitej 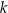 reszta z dzielenia liczby
reszta z dzielenia liczby 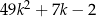 przez 7 jest równa 5.
przez 7 jest równa 5.
Klient wpłacił do banku 30 000 zł na lokatę dwuletnią. Po każdym rocznym okresie oszczędzania bank dolicza odsetki w wysokości 7% od kwoty bieżącego kapitału znajdującego się na lokacie. Po dwóch latach oszczędzania łączna wartość doliczonych odsetek na tej lokacie (bez uwzględniania podatków) jest równa
A) 2100 zł B) 2247 zł C) 4200 zł D) 4347 zł
Liczba 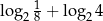 jest równa
jest równa
A) 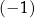 B)
B) 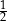 C) 2 D) 5
C) 2 D) 5
Liczba 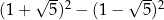 jest równa
jest równa
A) 0 B) 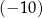 C)
C) 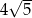 D)
D) 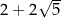
Dla każdej liczby rzeczywistej  różnej od 0 i 2 wyrażenie
różnej od 0 i 2 wyrażenie 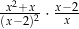 jest równe
jest równe
A) 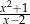 B)
B) 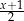 C)
C) 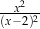 D)
D) 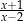
Rozwiąż nierówność 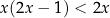 .
.
Rozwiąż równanie 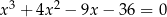 .
.
Równanie 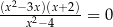 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania.
C) trzy rozwiązania. D) cztery rozwiązania.
W kartezjańskim układzie współrzędnych 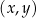 wykresy funkcji liniowych
wykresy funkcji liniowych 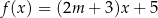 oraz
oraz 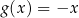 nie mają punktów wspólnych dla
nie mają punktów wspólnych dla
A) 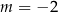 B)
B) 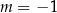 C)
C) 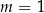 D)
D) 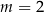
W kartezjańskim układzie współrzędnych 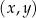 prosta o równaniu
prosta o równaniu 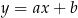 przechodzi przez punkty
przechodzi przez punkty 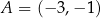 oraz
oraz 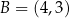 . Współczynnik
. Współczynnik  w równaniu tej prostej jest równy
w równaniu tej prostej jest równy
A) 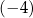 B)
B) 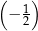 C) 2 D)
C) 2 D) 
Informacja do zadań 13.1 – 13.3
W kartezjańskim układzie współrzędnych 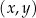 narysowano wykres funkcji
narysowano wykres funkcji 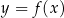 (zobacz rysunek).
(zobacz rysunek).
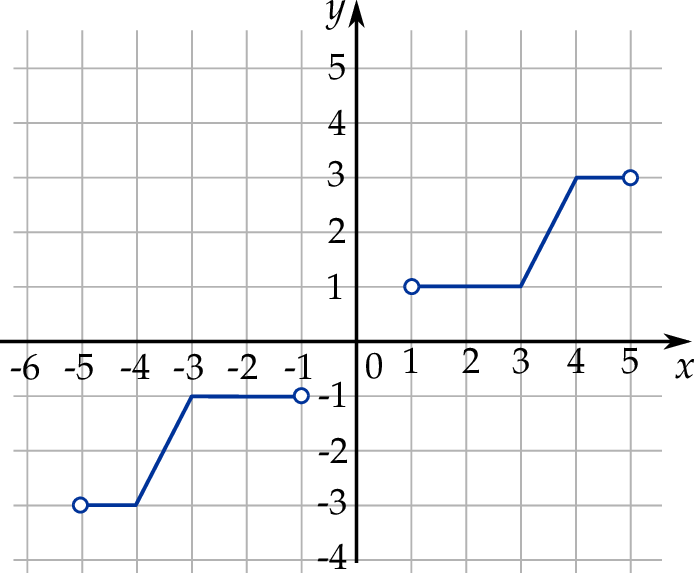
Dziedziną funkcji 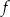 jest zbiór
jest zbiór
A) ![[− 3,− 1]∪ [1,3]](https://img.zadania.info/zes/0068777/HzesT44x.png) B)
B) 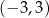 C)
C) 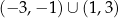
D) ![[− 5,− 1]∪ [1,5]](https://img.zadania.info/zes/0068777/HzesT47x.png) E)
E) 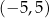 F)
F) 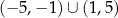
Zbiorem wartości funkcji 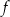 jest zbiór
jest zbiór
A) ![[− 3,− 1]∪ [1,3]](https://img.zadania.info/zes/0068777/HzesT51x.png) B)
B) 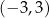 C)
C) 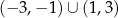
D) ![[− 5,− 1]∪ [1,5]](https://img.zadania.info/zes/0068777/HzesT54x.png) E)
E) 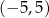 F)
F) 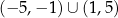
Zapisz poniżej zbiór wszystkich rozwiązań nierówności 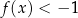 .
.
Funkcja kwadratowa 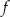 jest określona wzorem
jest określona wzorem 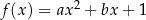 , gdzie
, gdzie  oraz
oraz 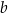 są pewnymi liczbami rzeczywistymi, takimi, że
są pewnymi liczbami rzeczywistymi, takimi, że 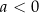 i
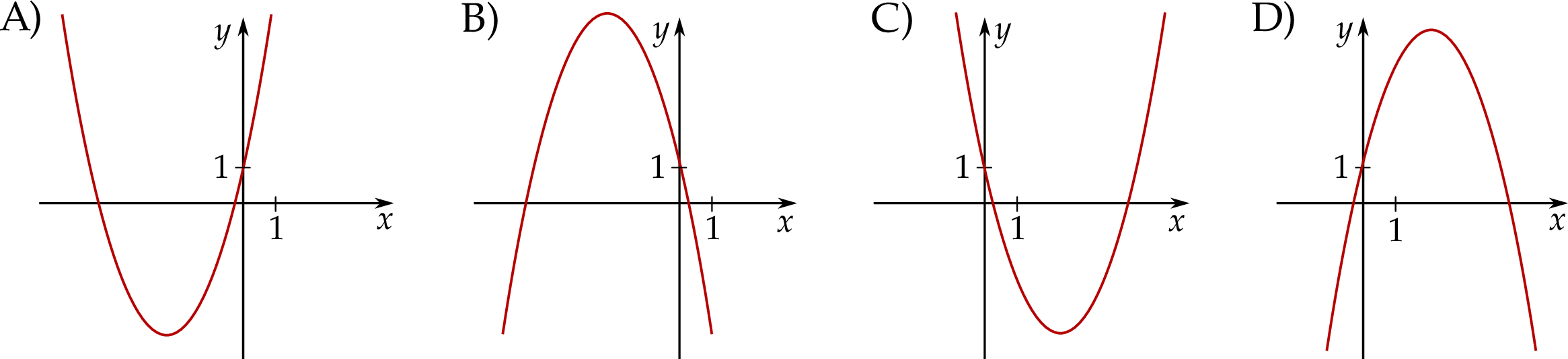
i 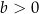 . Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych
. Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych 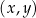 . Fragment wykresu funkcji
. Fragment wykresu funkcji 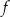 przedstawiono na rysunku
przedstawiono na rysunku
Informacja do zadań 15.1 i 15.2
Masa 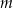 leku
leku 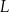 zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
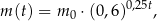
gdzie:
-
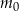 – masa (wyrażona w mg) przyjętej w chwili
– masa (wyrażona w mg) przyjętej w chwili 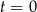 dawki leku,
dawki leku, -
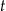 – czas (wyrażony w godzinach) liczony od momentu
– czas (wyrażony w godzinach) liczony od momentu 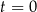 zażycia leku.
zażycia leku.
Chory przyjął jednorazowo lek 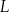 w dawce 200 mg. Oblicz, ile mg leku
w dawce 200 mg. Oblicz, ile mg leku 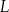 pozostanie w organizmie chorego po 12 godzinach od momentu przyjęcia dawki.
pozostanie w organizmie chorego po 12 godzinach od momentu przyjęcia dawki.
Liczby 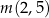 ,
, 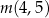 ,
, 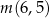 w podanej kolejności tworzą ciąg geometryczny. Oblicz iloraz tego ciągu.
w podanej kolejności tworzą ciąg geometryczny. Oblicz iloraz tego ciągu.
Ciąg 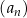 jest określony wzorem
jest określony wzorem 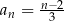 dla każdej liczby naturalnej
dla każdej liczby naturalnej 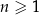 . Liczba wyrazów tego ciągu mniejszych od 10 jest równa
. Liczba wyrazów tego ciągu mniejszych od 10 jest równa
A) 28 B) 31 C) 32 D) 27
Trzywyrazowy ciąg 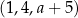 jest arytmetyczny. Liczba
jest arytmetyczny. Liczba  jest równa
jest równa
A) 0 B) 7 C) 2 D) 11
Ciąg geometryczny 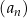 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 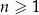 . W tym ciągu
. W tym ciągu 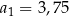 oraz
oraz 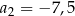 . Suma trzech początkowych wyrazów ciągu
. Suma trzech początkowych wyrazów ciągu 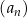 jest równa
jest równa
A) 11,25 B) 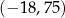 C) 15 D)
C) 15 D) 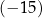
Dla każdego kąta ostrego  wyrażenie
wyrażenie 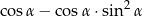 jest równe
jest równe
A) 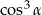 B)
B) 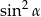 C)
C) 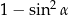 D)
D) 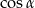
Dany jest trójkąt, którego kąty mają miary 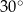 ,
, 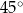 oraz
oraz 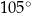 . Długości boków trójkąta, leżących naprzeciwko tych kątów są równe – odpowiednio –
. Długości boków trójkąta, leżących naprzeciwko tych kątów są równe – odpowiednio –  ,
, 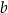 oraz
oraz  (zobacz rysunek).
(zobacz rysunek).

Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A–F. Pole tego trójkąta poprawnie określa wyrażenie
A) 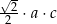 B)
B) 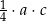 C)
C) 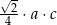
D) 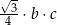 E)
E) 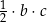 F)
F) 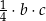
Odcinek 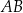 jest średnicą okręgu o środku
jest średnicą okręgu o środku 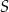 . Prosta
. Prosta 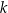 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 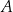 . Prosta
. Prosta 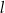 przecina ten okrąg w punktach
przecina ten okrąg w punktach 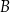 i
i 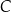 . Proste
. Proste 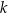 i
i 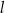 przecinają się w punkcie
przecinają się w punkcie 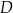 , przy czym
, przy czym 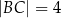 i
i 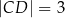 (zobacz rysunek).
(zobacz rysunek).

Odległość punktu 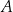 od prostej
od prostej 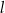 jest równa
jest równa
A) 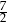 B) 5 C)
B) 5 C) 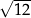 D)
D) 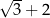
W trapezie 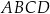 o podstawach
o podstawach 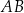 i
i 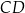 przekątne przecinają się w punkcie
przekątne przecinają się w punkcie 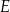 (zobacz rysunek).
(zobacz rysunek).
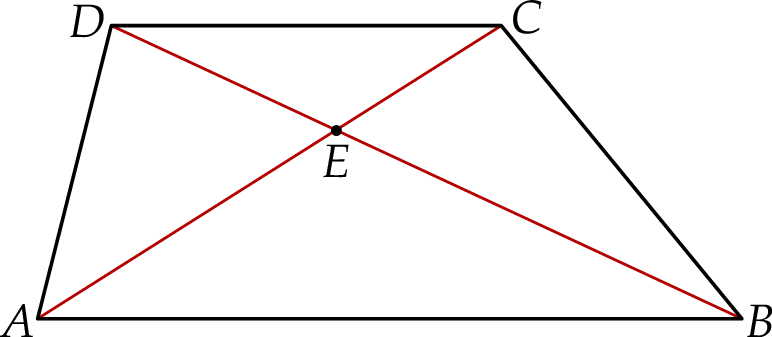
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 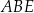 jest podobny do trójkąta jest podobny do trójkąta 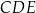 . . | P | F |
Pole trójkąta 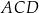 jest równe polu trójkąta jest równe polu trójkąta 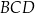 . . | P | F |
Na łukach 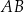 i
i 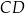 okręgu są oparte kąty wpisane
okręgu są oparte kąty wpisane 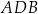 i
i 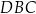 , takie, że
, takie, że 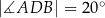 i
i 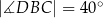 (zobacz rysunek). Cięciwy
(zobacz rysunek). Cięciwy 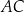 i
i 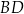 przecinają się w punkcie
przecinają się w punkcie 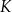 .
.

Miara kąta 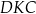 jest równa
jest równa
A) 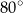 B)
B) 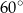 C)
C) 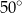 D)
D) 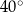
Pole trójkąta równobocznego 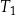 jest równe
jest równe 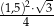 . Pole trójkąta równobocznego
. Pole trójkąta równobocznego 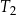 jest równe
jest równe 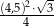 .
.
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1, 2 albo 3.
Trójkąt 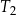 jest podobny do trójkąta
jest podobny do trójkąta 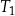 w skali
w skali
| A) 3, | B) 9, |
ponieważ
| 1) | każdy z tych trójkątów ma dokładnie trzy osie symetrii. |
| 2) | pole trójkąta 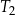 jest 9 razy większe od pola trójkąta jest 9 razy większe od pola trójkąta 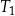 . . |
| 3) | bok trójkąta 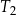 jest o 3 dłuższy od boku trójkąta jest o 3 dłuższy od boku trójkąta 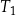 . . |
Pole równoległoboku 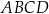 jest równe
jest równe 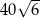 . Bok
. Bok 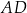 tego równoległoboku ma długość 10, a kąt
tego równoległoboku ma długość 10, a kąt 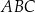 równoległoboku ma miarę
równoległoboku ma miarę 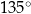 (zobacz rysunek).
(zobacz rysunek).

Długość boku 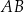 jest równa
jest równa
A) 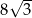 B)
B) 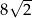 C)
C) 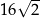 D)
D) 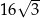
Funkcja liniowa 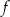 jest określona wzorem
jest określona wzorem 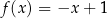 . Funkcja
. Funkcja 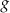 jest liniowa. W kartezjańskim układzie współrzędnych
jest liniowa. W kartezjańskim układzie współrzędnych 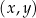 wykres funkcji
wykres funkcji 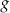 przechodzi przez punkt
przechodzi przez punkt 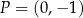 i jest prostopadły do wykresu funkcji
i jest prostopadły do wykresu funkcji 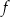 . Wzorem funkcji
. Wzorem funkcji 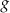 jest
jest
A) 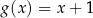 B)
B) 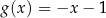 C)
C) 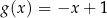 D)
D) 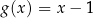
W kartezjańskim układzie współrzędnych 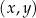 punkty
punkty 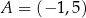 oraz
oraz 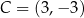 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 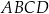 . Pole kwadratu
. Pole kwadratu 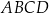 jest równe
jest równe
A) 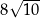 B)
B) 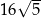 C) 40 D) 80
C) 40 D) 80
W kartezjańskim układzie współrzędnych 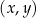 dane są punkty
dane są punkty 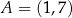 oraz
oraz 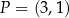 . Punkt
. Punkt 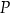 dzieli odcinek
dzieli odcinek 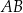 tak, że
tak, że 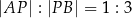 . Punkt
. Punkt 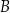 ma współrzędne
ma współrzędne
A) 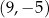 B)
B) 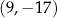 C)
C) 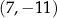 D)
D) 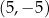
Informacja do zadań 29.1 i 29.2
Dany jest ostrosłup, którego podstawą jest kwadrat o boku 6. Jedna z krawędzi bocznych tego ostrosłupa ma długość 12 i jest prostopadła do płaszczyzny podstawy.
Oblicz objętość tego ostrosłupa.
Tangens kąta nachylenia najdłuższej krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy jest równy
A) 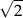 B)
B) 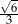 C)
C) 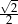 D)
D) 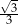
Dany jest graniastosłup prawidłowy sześciokątny 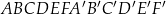 , w którym krawędź podstawy ma długość 5. Przekątna
, w którym krawędź podstawy ma długość 5. Przekątna 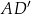 tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem 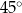 (zobacz rysunek).
(zobacz rysunek).
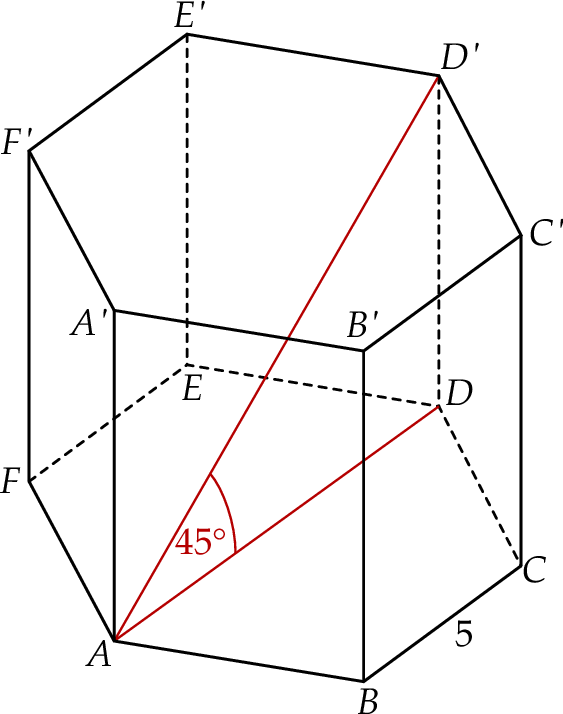
Pole ściany bocznej tego graniastosłupa jest równe
A) 12,5 B) 25 C) 50 D) 100
Wszystkich liczb naturalnych trzycyfrowych o sumie cyfr równej 3 jest
A) 8 B) 4 C) 5 D) 6
Ze zbioru ośmiu kolejnych liczb naturalnych – od 1 do 8 – losujemy kolejno bez zwracania dwa razy po jednej liczbie. Niech 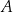 oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 8. Oblicz prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 8. Oblicz prawdopodobieństwo zdarzenia 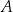 .
.
Działka ma kształt trapezu. Podstawy 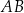 i
i 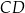 tego trapezu mają długości
tego trapezu mają długości 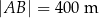 oraz
oraz 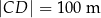 . Wysokość trapezu jest równa 75 m, a jego kąty
. Wysokość trapezu jest równa 75 m, a jego kąty 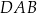 i
i 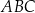 są ostre. Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie
są ostre. Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie 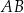 tego trapezu, a dwa pozostałe –
tego trapezu, a dwa pozostałe – 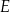 oraz
oraz 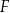 – na ramionach
– na ramionach 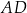 i
i 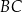 trapezu (zobacz rysunek).
trapezu (zobacz rysunek).

Wyznacz długości boków prostokąta, dla których powierzchnia wydzielonego placu będzie największa. Wyznacz tę największą powierzchnię.

