/Szkoła średnia/Zadania maturalne/Matura 2010
Przykładowe zadania
maturalne Matura 2010 poziom rozszerzony Informator CKE
1. Wykorzystanie i tworzenie informacji
Oblicz 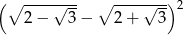 .
.
Miary dwóch kątów trójkąta wynoszą 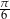 i
i 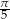 . Oblicz miarę trzeciego kąta. Odpowiedź podaj w stopniach.
. Oblicz miarę trzeciego kąta. Odpowiedź podaj w stopniach.
Dane jest równanie 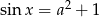 , z niewiadomą
, z niewiadomą  . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru  , dla których dane równanie nie ma rozwiązań.
, dla których dane równanie nie ma rozwiązań.
Wyznacz miejsca zerowe funkcji
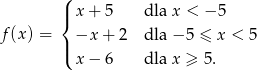
2. Wykorzystanie i interpretowanie reprezentacji
Rozwiąż równanie 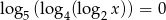 .
.
Funkcja 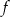 jest określona wzorem
jest określona wzorem 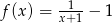 dla wszystkich liczb rzeczywistych
dla wszystkich liczb rzeczywistych 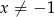 . Rozwiąż nierówność
. Rozwiąż nierówność 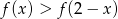 .
.
Narysuj wykres funkcji 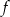 określonej w przedziale
określonej w przedziale 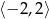 wzorem
wzorem 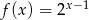 .
.
Pole wycinka koła o promieniu 3 cm jest równe 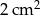 . Oblicz miarę łukową kąta środkowego tego wycinka.
. Oblicz miarę łukową kąta środkowego tego wycinka.
Punkty 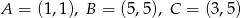 są wierzchołkami trapezu równoramiennego
są wierzchołkami trapezu równoramiennego 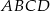 niebędącego równoległobokiem, w którym
niebędącego równoległobokiem, w którym 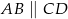 .
.
- Wyznacz równanie osi symetrii tego trapezu.
- Oblicz pole tego trapezu.
Na okręgu zaznaczono sześć różnych punktów. Ile różnych wielokątów wypukłych o wszystkich wierzchołkach w tych punktach można narysować?
Dla jakich wartości parametru 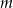 reszta z dzielenia wielomianu
reszta z dzielenia wielomianu
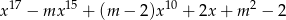
przez dwumian 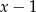 jest równa 3?
jest równa 3?
Wyznacz równanie okręgu o środku 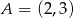 , stycznego do prostej o równaniu
, stycznego do prostej o równaniu 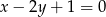 .
.
3. Modelowanie matematyczne
Niech 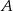 będzie zbiorem wszystkich liczb
będzie zbiorem wszystkich liczb  , które spełniają równość
, które spełniają równość 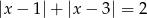 . Niech
. Niech 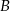 będzie zbiorem wszystkich punktów na osi liczbowej, których suma odległości od punktów 4 i 6 jest niewiększa niż 4. Zaznacz na osi liczbowej zbiory
będzie zbiorem wszystkich punktów na osi liczbowej, których suma odległości od punktów 4 i 6 jest niewiększa niż 4. Zaznacz na osi liczbowej zbiory 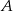 i
i 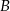 oraz wszystkie punkty, które należą jednocześnie do
oraz wszystkie punkty, które należą jednocześnie do 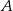 i do
i do 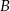 .
.
Wiedząc, że przedział 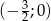 jest zbiorem wszystkich rozwiązań nierówności
jest zbiorem wszystkich rozwiązań nierówności 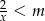 z niewiadomą
z niewiadomą  , oblicz
, oblicz 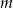 .
.
Rozpatrujemy wszystkie prostokąty o polu równym 6, których dwa sąsiednie boki zawarte są w osiach 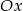 i
i 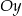 układu współrzędnych. Wyznacz równanie krzywej będącej zbiorem tych wierzchołków rozpatrywanych prostokątów, które nie leżą na żadnej z osi układu współrzędnych. Narysuj tę krzywą.
układu współrzędnych. Wyznacz równanie krzywej będącej zbiorem tych wierzchołków rozpatrywanych prostokątów, które nie leżą na żadnej z osi układu współrzędnych. Narysuj tę krzywą.
Miary pięciu kątów tworzą ciąg arytmetyczny. Drugim wyrazem tego ciągu jest 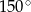 , a czwartym
, a czwartym 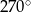 . Oblicz sumę sinusów tych pięciu kątów.
. Oblicz sumę sinusów tych pięciu kątów.
Dane jest równanie 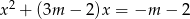 z niewiadomą
z niewiadomą  . Sformułuj warunki, jakie powinien spełniać parametr
. Sformułuj warunki, jakie powinien spełniać parametr 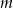 , by to równanie miało dwa różne pierwiastki, których suma odwrotności jest dodatnia.
, by to równanie miało dwa różne pierwiastki, których suma odwrotności jest dodatnia.
Wyznacz pierwsze trzy wyrazy ciągu geometrycznego wiedząc, że są one dodatnie, ich suma jest równa 21 oraz suma ich odwrotności jest równa 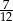 .
.
Z szuflady, w której znajduje się 10 różnych par rękawiczek wybieramy losowo cztery rękawiczki. Opisz zbiór wszystkich zdarzeń elementarnych, a następnie oblicz prawdopodobieństwa zdarzeń:
A – wśród wylosowanych rękawiczek nie będzie pary,
B – wśród wylosowanych rękawiczek będzie dokładnie jedna para.
4. Użycie i tworzenie strategii
Wyznacz wszystkie wartości parametru 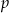 , dla których równanie
, dla których równanie 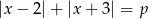 ma dokładnie dwa rozwiązania.
ma dokładnie dwa rozwiązania.
Wykaż, że dla 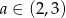 zachodzi równość
zachodzi równość 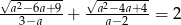 .
.
Dane jest równanie 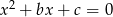 z niewiadomą
z niewiadomą  . Wyznacz wartości
. Wyznacz wartości 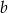 i
i  tak, by były one rozwiązaniami danego równania.
tak, by były one rozwiązaniami danego równania.
Dane są funkcje liniowe 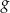 i
i 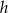 określone wzorami:
określone wzorami: 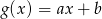 i
i 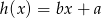 . Wiadomo, że funkcja
. Wiadomo, że funkcja 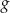 jest rosnąca, a
jest rosnąca, a 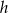 malejąca.
malejąca.
- Wyznacz pierwszą współrzędna punktu przecięcia wykresów tych funkcji.
- Oblicz liczby
 i
i 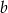 wiedząc, że wykresy funkcji
wiedząc, że wykresy funkcji 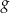 i
i 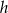 są prostymi prostopadłymi, a punkt ich przecięcia leży na osi
są prostymi prostopadłymi, a punkt ich przecięcia leży na osi 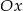 .
.
Dany jest ciąg 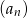 mający tę własność, że dla każdej liczby naturalnej
mający tę własność, że dla każdej liczby naturalnej  suma
suma  początkowych wyrazów tego ciągu jest równa
początkowych wyrazów tego ciągu jest równa 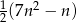 . Oblicz dwudziesty wyraz tego ciągu. Wykaż, że
. Oblicz dwudziesty wyraz tego ciągu. Wykaż, że 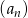 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym.
Proste zawierające ramiona 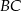 i
i 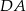 trapezu
trapezu 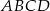 przecinają się w punkcie
przecinają się w punkcie 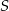 . Dane są:
. Dane są: 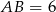 ,
, 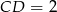 oraz obwód trójkąta
oraz obwód trójkąta 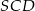 równy
równy 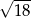 . Oblicz obwód trójkąta
. Oblicz obwód trójkąta 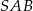 .
.
W pewnym trapezie kąty przy dwóch przeciwległych wierzchołkach mają miary  oraz
oraz 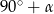 . Jedno z ramion tego trapezu ma długość
. Jedno z ramion tego trapezu ma długość 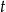 . Wyznacz różnicę długości podstaw tego trapezu.
. Wyznacz różnicę długości podstaw tego trapezu.
Czworokąt 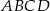 jest wpisany w okrąg. Dane są
jest wpisany w okrąg. Dane są 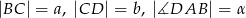 . Wyznacz długość przekątnej
. Wyznacz długość przekątnej 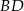 .
.
Podstawą ostrosłupa 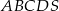 jest kwadrat
jest kwadrat 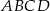 o boku długości 4. Odcinek
o boku długości 4. Odcinek 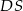 jest wysokością ostrosłupa i ma długość 6. Punkt
jest wysokością ostrosłupa i ma długość 6. Punkt 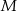 jest środkiem odcinka
jest środkiem odcinka 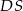 . Oblicz pole przekroju ostrosłupa płaszczyzną
. Oblicz pole przekroju ostrosłupa płaszczyzną 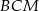 .
.
Ze zbioru liczb 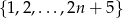 wybieramy jednocześnie dwie liczby (nie uwzględniamy kolejności). Na ile sposobów możemy to zrobić, tak aby otrzymać dwie liczby takie, że:
wybieramy jednocześnie dwie liczby (nie uwzględniamy kolejności). Na ile sposobów możemy to zrobić, tak aby otrzymać dwie liczby takie, że:
- ich różnica będzie liczbą parzystą,
- suma ich kwadratów będzie liczbą podzielną przez cztery?
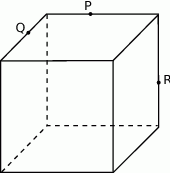
Narysuj przekrój równoległościanu płaszczyzną 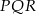 .
.
Wiedząc, że dla sum częściowych pewnego ciągu geometrycznego o wyrazach dodatnich prawdziwa jest równość 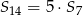 , oblicz iloraz tego ciągu.
, oblicz iloraz tego ciągu.
5. Rozumowanie i argumentacja
Wielomian 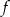 jest określony wzorem
jest określony wzorem 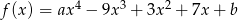 dla pewnych liczb pierwszych
dla pewnych liczb pierwszych  oraz
oraz 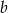 . Wiadomo, ze liczba
. Wiadomo, ze liczba 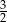 jest pierwiastkiem tego wielomianu. Oblicz
jest pierwiastkiem tego wielomianu. Oblicz  i
i 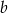 .
.
Uzasadnij, że dla dowolnej liczby całkowitej 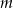 rozwiązania równania
rozwiązania równania 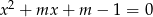 z niewiadomą
z niewiadomą  są liczbami całkowitymi.
są liczbami całkowitymi.
Funkcja 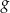 jest określona w zbiorze wszystkich liczb rzeczywistych w następujący sposób: jeśli
jest określona w zbiorze wszystkich liczb rzeczywistych w następujący sposób: jeśli 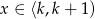 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej 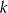 , to
, to 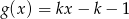 .
.
- Narysuj wykres funkcji
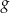 w przedziale
w przedziale 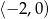 .
. - Uzasadnij, że funkcja
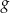 nie ma miejsc zerowych.
nie ma miejsc zerowych. - Rozwiąż równanie
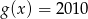 .
.
Wykaż, że jeżeli liczby 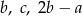 są kolejnymi wyrazami ciągu geometrycznego to liczby
są kolejnymi wyrazami ciągu geometrycznego to liczby 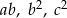 są kolejnymi wyrazami ciągu arytmetycznego.
są kolejnymi wyrazami ciągu arytmetycznego.
Wykaż, że wyrażenie 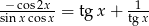 nie jest tożsamością.
nie jest tożsamością.
Dany jest taki czworokąt wypukły 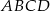 , że okręgi wpisane w trójkąty
, że okręgi wpisane w trójkąty 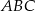 i
i 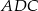 są styczne. Wykaż, że w czworokąt
są styczne. Wykaż, że w czworokąt 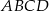 można wpisać okrąg.
można wpisać okrąg.
Dane są punkty 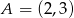 i
i 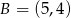 . Na prostej o równaniu
. Na prostej o równaniu 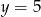 wyznacz punkt
wyznacz punkt 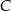 tak, aby łamana
tak, aby łamana 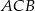 miała jak najmniejszą długość. Odpowiedź uzasadnij.
miała jak najmniejszą długość. Odpowiedź uzasadnij.
Trójkąt 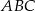 jest podstawą ostrosłupa
jest podstawą ostrosłupa 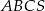 . Punkt
. Punkt 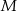 jest środkiem boku
jest środkiem boku 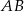 i
i 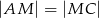 . Odcinek
. Odcinek 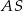 jest wysokością tego ostrosłupa. Wykaż, że kąt
jest wysokością tego ostrosłupa. Wykaż, że kąt 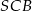 jest prosty.
jest prosty.
Podstawą ostrosłupa 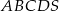 jest prostokąt
jest prostokąt 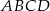 , w którym
, w którym 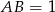 ,
, 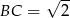 . Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz wartość dowolnej funkcji trygonometrycznej kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.
. Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz wartość dowolnej funkcji trygonometrycznej kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.
Tabela zawiera niektóre wyniki pisemnego sprawdzianu z matematyki w pewnej klasie maturalnej (ocenionego w sześciostopniowej skali ocen).
| Dziewczęta | Chłopcy | |
| liczba osób | 11 | 14 |
| średnia ocen | 4,0 | 3,8 |
| odchylenie standardowe | 1,1 | 1,8 |
Oblicz średnią ocen z tego sprawdzianu oraz odchylenie standardowe dla całej klasy. Wyniki podaj z zaokrągleniem do jednego miejsca po przecinku.

