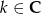/Szkoła średnia/Równania

Zadanie nr 9287456

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 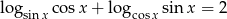logsinxco sx + logcosxsin x = 2 .

Rozwiązanie

Ze względu na dziedzinę logarytmy musimy założyć, że 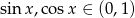sin x,cos x ∈ (0,1) . Przy tym założeniu możemy skorzystać ze wzoru na zmianę podstawy logarytmu.

logsinxcos x + logcosxsin x = 2 log sin x logsinxcos x + ---sinx----- = 2 logsinxcos x ------1----- logsinxcos x + log cos x = 2. sinx

Podstawiamy teraz 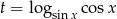t = logsin xcos x .

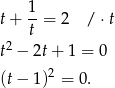
1 t+ --= 2 / ⋅t 2 t t − 2t+ 1 = 0 (t− 1)2 = 0.

Zatem 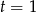t = 1 i mamy

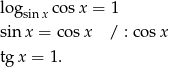
log cosx = 1 sinx sin x = co sx / : cosx tg x = 1 .

Szkicujemy tangens.

PIC

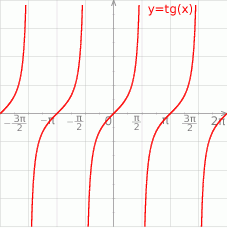
Ponieważ założyliśmy, że 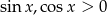sin x,cos x > 0 , więc szukamy rozwiązań tylko I ćwiartce. Stąd

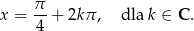
π x = -- + 2kπ , dla k ∈ C . 4

 
Odpowiedź: 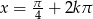x = π4-+ 2kπ , gdzie k ∈ C

Wersja PDF