Dany jest rosnący ciąg geometryczny 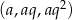 , którego wszystkie wyrazy i iloraz są liczbami całkowitymi nieparzystymi. Jeśli największy wyraz ciągu zmniejszymy o 4, to otrzymamy ciąg arytmetyczny. Oblicz wyraz
, którego wszystkie wyrazy i iloraz są liczbami całkowitymi nieparzystymi. Jeśli największy wyraz ciągu zmniejszymy o 4, to otrzymamy ciąg arytmetyczny. Oblicz wyraz 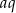 tego ciągu.
tego ciągu.
/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny
Dany jest malejący ciąg geometryczny 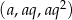 , którego wszystkie wyrazy i iloraz są liczbami całkowitymi niepodzielnymi przez 3. Jeśli najmniejszy wyraz ciągu zwiększymy o 18, to otrzymamy ciąg arytmetyczny. Oblicz wyraz
, którego wszystkie wyrazy i iloraz są liczbami całkowitymi niepodzielnymi przez 3. Jeśli najmniejszy wyraz ciągu zwiększymy o 18, to otrzymamy ciąg arytmetyczny. Oblicz wyraz 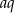 tego ciągu.
tego ciągu.
Ciąg 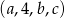 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 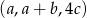 jest geometryczny. Oblicz
jest geometryczny. Oblicz 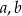 i
i  .
.
Liczby 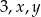 są kolejnymi wyrazami ciągu arytmetycznego. Jeśli liczbę
są kolejnymi wyrazami ciągu arytmetycznego. Jeśli liczbę  zmniejszymy o 5, a liczbę
zmniejszymy o 5, a liczbę 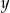 zwiększymy o 17, to otrzymane liczby będą kolejnymi wyrazami ciągu geometrycznego. Wyznacz wartości liczbowe
zwiększymy o 17, to otrzymane liczby będą kolejnymi wyrazami ciągu geometrycznego. Wyznacz wartości liczbowe  i
i 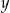 .
.
Liczby 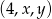 są kolejnymi wyrazami ciągu arytmetycznego. Jeśli liczbę
są kolejnymi wyrazami ciągu arytmetycznego. Jeśli liczbę  zwiększymy o 1, a liczbę
zwiększymy o 1, a liczbę 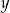 zwiększymy o 3, to otrzymane liczby będą kolejnymi wyrazami ciągu geometrycznego. Wyznacz
zwiększymy o 3, to otrzymane liczby będą kolejnymi wyrazami ciągu geometrycznego. Wyznacz  i
i 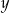 .
.
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 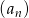 wyraża się wzorem
wyraża się wzorem 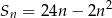 , gdzie
, gdzie 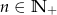 . Oblicz
. Oblicz  wiedząc, że liczby:
wiedząc, że liczby: 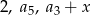 w podanej kolejności tworzą ciąg geometryczny.
w podanej kolejności tworzą ciąg geometryczny.
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 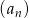 wyraża się wzorem
wyraża się wzorem 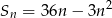 , gdzie
, gdzie 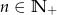 . Oblicz
. Oblicz  wiedząc, że liczby:
wiedząc, że liczby: 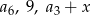 w podanej kolejności tworzą ciąg geometryczny.
w podanej kolejności tworzą ciąg geometryczny.
Między liczby 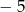 i 49 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.
i 49 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.
Między liczby 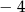 i 36 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.
i 36 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.
Czterowyrazowy ciąg 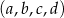 jest rosnący i arytmetyczny. Suma kwadratów trzech najmniejszych wyrazów tego ciągu jest pięciokrotnie większa od kwadratu czwartego wyrazu. Ponadto ciąg
jest rosnący i arytmetyczny. Suma kwadratów trzech najmniejszych wyrazów tego ciągu jest pięciokrotnie większa od kwadratu czwartego wyrazu. Ponadto ciąg 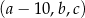 jest geometryczny. Oblicz wyrazy ciągu
jest geometryczny. Oblicz wyrazy ciągu 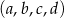 .
.
Czterowyrazowy ciąg 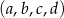 jest rosnący i arytmetyczny. Kwadrat największego wyrazu tego ciągu jest równy podwojonej sumie kwadratów pozostałych wyrazów tego ciągu. Ponadto ciąg
jest rosnący i arytmetyczny. Kwadrat największego wyrazu tego ciągu jest równy podwojonej sumie kwadratów pozostałych wyrazów tego ciągu. Ponadto ciąg 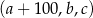 jest geometryczny. Oblicz wyrazy ciągu
jest geometryczny. Oblicz wyrazy ciągu 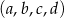 .
.
Czterowyrazowy ciąg 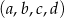 jest rosnący i arytmetyczny. Kwadrat największego wyrazu tego ciągu jest równy podwojonej sumie kwadratów pozostałych wyrazów tego ciągu. Ponadto ciąg
jest rosnący i arytmetyczny. Kwadrat największego wyrazu tego ciągu jest równy podwojonej sumie kwadratów pozostałych wyrazów tego ciągu. Ponadto ciąg 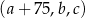 jest geometryczny. Oblicz wyrazy ciągu
jest geometryczny. Oblicz wyrazy ciągu 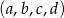 .
.
Trzy liczby tworzą ciąg arytmetyczny o 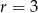 . Jeżeli pierwszą powiększymy o 8 drugą o 6 a trzecią pozostawimy bez zmian to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Znajdź te liczby.
. Jeżeli pierwszą powiększymy o 8 drugą o 6 a trzecią pozostawimy bez zmian to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Znajdź te liczby.
Trzy liczby tworzą ciąg arytmetyczny o 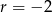 . Jeżeli pierwszą powiększymy o 3 drugą o 1 a trzecią pozostawimy bez zmian to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Znajdź te liczby.
. Jeżeli pierwszą powiększymy o 3 drugą o 1 a trzecią pozostawimy bez zmian to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Znajdź te liczby.
Trzy liczby, których suma jest równa 93, tworzą ciąg geometryczny. Te same liczby stanowią pierwszy, drugi oraz siódmy wyraz ciągu arytmetycznego. Wyznacz te liczby.
Trzy liczby tworzą rosnący ciąg geometryczny. Suma tych liczb jest równa 28. Liczby te są jednocześnie 1, 2 i 4 wyrazem ciągu arytmetycznego. Jakie to liczby?
Liczby 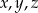 w podanej kolejności, tworzą ciąg geometryczny. Suma tych liczb wynosi 13. Te same liczby, w podanej kolejności, są odpowiednio pierwszym, drugim i piątym wyrazem ciągu arytmetycznego. Wyznacz,
w podanej kolejności, tworzą ciąg geometryczny. Suma tych liczb wynosi 13. Te same liczby, w podanej kolejności, są odpowiednio pierwszym, drugim i piątym wyrazem ciągu arytmetycznego. Wyznacz, 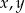 oraz
oraz  .
.
Trzywyrazowy ciąg 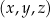 jest geometryczny i rosnący. Suma wyrazów tego ciągu jest równa 105. Liczby
jest geometryczny i rosnący. Suma wyrazów tego ciągu jest równa 105. Liczby 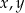 oraz
oraz  są – odpowiednio – pierwszym, drugim oraz szóstym wyrazem ciągu arytmetycznego
są – odpowiednio – pierwszym, drugim oraz szóstym wyrazem ciągu arytmetycznego 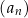 , określonego dla każdej liczby naturalnej
, określonego dla każdej liczby naturalnej 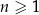 . Oblicz
. Oblicz 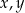 oraz
oraz  .
.
W trzywyrazowym ciągu geometrycznym 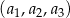 spełniona jest równość
spełniona jest równość 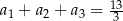 . Wyrazy
. Wyrazy 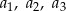 są – odpowiednio – dziewiątym, trzecim i pierwszym wyrazem rosnącego ciągu arytmetycznego. Oblicz
są – odpowiednio – dziewiątym, trzecim i pierwszym wyrazem rosnącego ciągu arytmetycznego. Oblicz 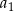 .
.
W trzywyrazowym ciągu geometrycznym 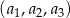 spełniona jest równość
spełniona jest równość 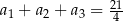 . Wyrazy
. Wyrazy 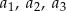 są – odpowiednio – czwartym, drugim i pierwszym wyrazem rosnącego ciągu arytmetycznego. Oblicz
są – odpowiednio – czwartym, drugim i pierwszym wyrazem rosnącego ciągu arytmetycznego. Oblicz  .
.
Trzy liczby, których suma jest równa 105, są kolejnymi wyrazami rosnącego ciągu geometrycznego. Pierwsza z tych liczb jest jednocześnie pierwszym, druga szóstym, a trzecia dwudziestym szóstym wyrazem pewnego ciągu arytmetycznego. Oblicz te liczby.
Cztery liczby tworzą ciąg geometryczny. Jeżeli od pierwszej z nich odejmiemy 2, od drugiej 3, od trzeciej 9, a od czwartej 25, to otrzymane różnice utworzą ciąg arytmetyczny. Znajdź te liczby.
Trzy liczby są kolejnymi wyrazami ciągu arytmetycznego. Ich suma wynosi 18. Jeśli największą z tych liczb zwiększymy o 8, a pozostałych nie zmienimy, to uzyskamy trzy kolejne wyrazy ciągu geometrycznego. Wyznacz te liczby.
Trzy liczby są kolejnymi wyrazami ciągu arytmetycznego. Ich suma wynosi 27. Jeśli największą z tych liczb zwiększymy o 12, a pozostałych nie zmienimy, to uzyskamy trzy kolejne wyrazy ciągu geometrycznego. Wyznacz te liczby.
Trzy liczby tworzą ciąg geometryczny. Jeżeli drugą z nich zwiększymy o 8, to otrzymamy ciąg arytmetyczny. Jeżeli trzeci wyraz otrzymanego ciągu arytmetycznego zwiększymy o 64 to znów otrzymamy ciąg geometryczny. Wyznacz te liczby.
Trzy liczby są kolejnymi wyrazami ciągu geometrycznego, którego iloraz jest różny od 1. Jeżeli weźmiemy kolejno drugą z nich, pierwszą i trzecią, to otrzymamy trzy kolejne wyrazy ciągu arytmetycznego. Jeżeli pierwszy wyraz tego ciągu arytmetycznego zmniejszymy o 7, drugi pozostawimy bez zmian, a trzeci zwiększymy o 3, to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Oblicz te liczby.
Wykaż, że jeżeli ciąg 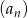 jest ciągiem geometrycznym o wyrazach dodatnich, to ciąg o wyrazie ogólnym
jest ciągiem geometrycznym o wyrazach dodatnich, to ciąg o wyrazie ogólnym 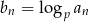 , dla
, dla 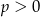 i
i 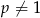 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym.
Ciąg 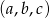 jest geometryczny, a ciągi
jest geometryczny, a ciągi 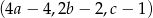 i
i 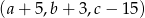 są arytmetyczne. Oblicz
są arytmetyczne. Oblicz 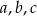 .
.
Ciąg  jest geometryczny, a ciągi
jest geometryczny, a ciągi 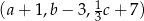 i
i 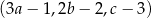 są arytmetyczne. Oblicz
są arytmetyczne. Oblicz 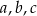 .
.
Trzy liczby o sumie 7 tworzą ciąg geometryczny. Jeżeli do drugiej liczby dodamy pierwszą to ciąg zmieni się w arytmetyczny. Wyznacz pierwszą z tych liczb. Uwzględnij wszystkie możliwości.
Ciąg 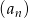 dany jest wzorem
dany jest wzorem 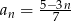 , dla
, dla 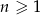 .
.
- Oblicz sumę
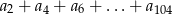 .
. - Ustalmy
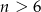 . Dla jakich
. Dla jakich  liczby
liczby 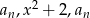 są kolejnymi wyrazami ciągu geometrycznego?
są kolejnymi wyrazami ciągu geometrycznego?
Dane są dwa ciągi rosnące: arytmetyczny 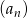 i geometryczny
i geometryczny 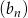 . Pierwsze wyrazy obu ciągów są równe 2, trzecie ich wyrazy są takie same, a jedenasty wyraz ciągu arytmetycznego jest równy piątemu wyrazowi ciągu geometrycznego. Wyznacz te ciągi zapisując wzory na wyrazy ogólne.
. Pierwsze wyrazy obu ciągów są równe 2, trzecie ich wyrazy są takie same, a jedenasty wyraz ciągu arytmetycznego jest równy piątemu wyrazowi ciągu geometrycznego. Wyznacz te ciągi zapisując wzory na wyrazy ogólne.
Ciąg 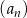 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 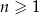 , jest geometryczny i ma wszystkie wyrazy dodatnie. Ponadto
, jest geometryczny i ma wszystkie wyrazy dodatnie. Ponadto 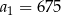 i
i 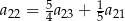 . Ciąg
. Ciąg 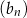 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 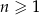 , jest arytmetyczny. Suma wszystkich wyrazów ciągu
, jest arytmetyczny. Suma wszystkich wyrazów ciągu 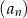 jest równa sumie dwudziestu pięciu początkowych kolejnych wyrazów ciągu
jest równa sumie dwudziestu pięciu początkowych kolejnych wyrazów ciągu 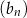 . Ponadto
. Ponadto 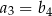 . Oblicz
. Oblicz 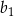 .
.
Trzy liczby tworzą ciąg arytmetyczny. Jeśli do pierwszej z nich dodamy 5, do drugiej 3, a do trzeciej 4, to otrzymamy rosnący ciąg geometryczny, w którym trzeci wyraz jest cztery razy większy od pierwszego. Znajdź te liczby.
Ciąg 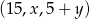 jest arytmetyczny, natomiast ciąg
jest arytmetyczny, natomiast ciąg 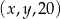 jest geometryczny. Oblicz
jest geometryczny. Oblicz  oraz
oraz 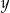 i podaj ten ciąg geometryczny.
i podaj ten ciąg geometryczny.
Ciąg 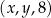 jest malejącym ciągiem geometrycznym. Jeżeli pierwszy wyraz tego ciągu zmniejszymy o 2, to otrzymamy trzywyrazowy ciąg arytmetyczny. Wyznacz
jest malejącym ciągiem geometrycznym. Jeżeli pierwszy wyraz tego ciągu zmniejszymy o 2, to otrzymamy trzywyrazowy ciąg arytmetyczny. Wyznacz  i
i 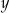 .
.
Dane są 4 liczby, z których 3 pierwsze tworzą ciąg geometryczny, a 3 ostatnie tworzą ciąg arytmetyczny. Suma pierwszej i czwartej wynosi 14, a suma drugiej i trzeciej wynosi 12. Wyznacz te 4 liczby.
Dane są 4 liczby, z których 3 pierwsze tworzą ciąg geometryczny, a 3 ostatnie tworzą ciąg arytmetyczny. Suma pierwszej i czwartej wynosi 22, a suma drugiej i trzeciej wynosi 4. Wyznacz te 4 liczby.
- Wyznacz liczbę naturalną
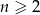 , dla której liczby
, dla której liczby 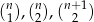 są kolejnymi wyrazami ciągu arytmetycznego;
są kolejnymi wyrazami ciągu arytmetycznego; - Dla wyznaczonej wartości
 , wyznacz liczbę naturalną
, wyznacz liczbę naturalną 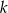 tak, aby liczby
tak, aby liczby 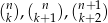 były kolejnymi wyrazami ciągu geometrycznego.
były kolejnymi wyrazami ciągu geometrycznego.

