/Szkoła średnia/Geometria

Zadanie nr 6539130

Dodaj do ulubionych
Dodaj do rozwiązanych

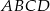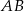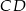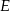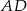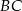W trapezie ABCD podstawa AB jest 3 razy dłuższa od podstawy CD . Przekątne tego trapezu przecinają się w punkcie E , a proste zawierające ramiona AD i BC przecinają się w punkcie 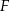F . Oblicz stosunek pola czworokąta 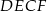DECF do pola trapezu ABCD .

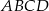Rozwiązanie

Rozpoczynamy oczywiście od rysunku.

PIC

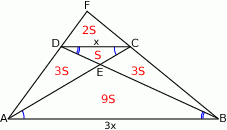
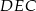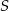Oznaczmy pole trójkąta DEC przez S . Spróbujemy (w zależności od 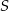S ) wyliczyć pola wszystkich trójkątów na obrazku.

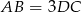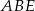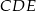Wiemy, że AB = 3DC , więc trójkąty ABE i CDE są podobne (bo mają równe kąty) w skali 3:1. Zatem

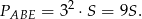
2 PABE = 3 ⋅S = 9S.

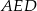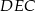Trójkąty AED i DEC mają wspólną wysokość opuszczoną na prostą 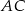AC , a stosunek ich podstaw jest równy 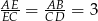AE AB EC-= CD- = 3 . Zatem

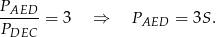
P --AED-= 3 ⇒ PAED = 3S. PDEC

Dokładnie w ten sam sposób uzasadniamy, że 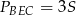PBEC = 3S .

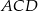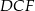Teraz popatrzmy na trójkąty ACD i DCF . Mają one wspólną wysokość opuszczoną na prostą 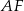AF oraz stosunek ich podstaw jest równy

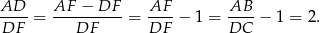
AD-- AF-−--DF-- AF-- AB-- DF = DF = DF − 1 = DC − 1 = 2.

Zatem

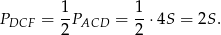
P = 1-P = 1-⋅4S = 2S . DCF 2 ACD 2

Mamy więc

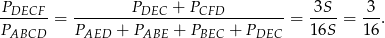
PDECF-- --------PDEC-+--PCFD--------- -3S- -3- PABCD = PAED + PABE + PBEC + PDEC = 16S = 16 .

 
Odpowiedź: -3 16

Wersja PDF