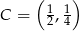Zadanie nr 7805060
Dane są punkty 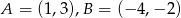 . Wyznacz taki punkt
. Wyznacz taki punkt 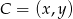 , gdzie
, gdzie 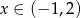 leżący na paraboli o równaniu
leżący na paraboli o równaniu 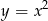 , aby pole trójkąta
, aby pole trójkąta 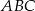 było największe.
było największe.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
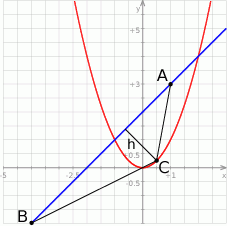
Szukamy punktu 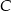 postaci
postaci 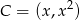 .
.
Sposób I
Korzystamy ze wzoru na pole trójkąta o wierzchołkach 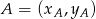 ,
, 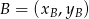 i
i 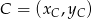 .
.
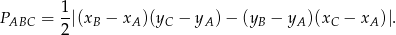
W naszym przypadku mamy
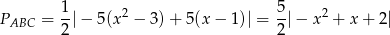
Ustalmy jaki jest znak wyrażenia pod wartością bezwzględną.
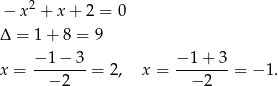
Zatem na przedziale 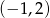 wyrażenie to jest dodatnie i mamy
wyrażenie to jest dodatnie i mamy
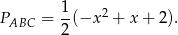
Otrzymana parabola przyjmuje największą wartość w wierzchołku, czyli dla
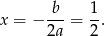
Otrzymujemy wtedy 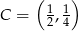 .
.
Sposób II
Ponieważ punkty 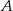 i
i 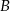 są ustalone, pole trójkąta
są ustalone, pole trójkąta 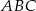 będzie największe, gdy odległość punktu
będzie największe, gdy odległość punktu 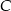 od prostej
od prostej 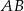 będzie największa. Napiszmy równanie prostej
będzie największa. Napiszmy równanie prostej 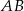 . Szukamy prostej w postaci
. Szukamy prostej w postaci 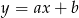 . Podstawiając współrzędne punktów
. Podstawiając współrzędne punktów 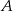 i
i 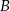 otrzymujemy układ równań
otrzymujemy układ równań
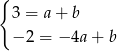
Odejmując od pierwszego równania drugie otrzymujemy
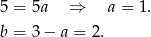
Zatem prosta  ma równanie
ma równanie 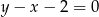 . Korzystamy teraz ze wzoru na odległość punktu od prostej, aby obliczyć odległość punktu
. Korzystamy teraz ze wzoru na odległość punktu od prostej, aby obliczyć odległość punktu 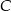 od prostej
od prostej 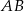 (czyli długość wysokości trójkąta
(czyli długość wysokości trójkąta 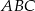 opuszczonej na bok
opuszczonej na bok 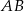 ).
).
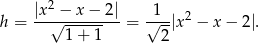
Ustalmy jaki jest znak wyrażenia pod wartością bezwzględną.
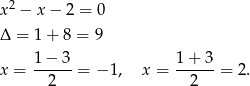
Zatem na przedziale 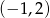 wyrażenie to jest ujemne i mamy
wyrażenie to jest ujemne i mamy
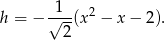
Otrzymana parabola przyjmuje największą wartość w wierzchołku, czyli dla
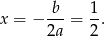
Otrzymujemy wtedy 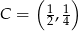 .
.
Odpowiedź: