/Szkoła średnia/Nierówności/Udowodnij.../Wielomianowe

Zadanie nr 1709598

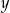Wykaż, że dla każdej liczby rzeczywistej x oraz dla każdej liczby rzeczywistej y , spełniających warunek 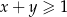x + y ≥ 1 , prawdziwa jest nierówność

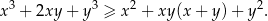
x3 + 2xy + y3 ≥ x2 + xy (x+ y)+ y2.
Wersja PDF

Rozwiązanie

Sposób I

Przekształcamy nierówność w sposób równoważny – rzuca się w niej w oczy kilka wzorów skróconego mnożenia.

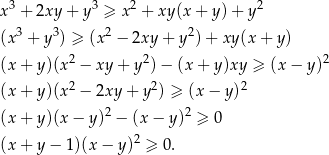
3 3 2 2 x + 2xy + y ≥ x + xy(x + y )+ y (x 3 + y3) ≥ (x2 − 2xy + y2)+ xy(x + y ) (x + y )(x 2 − xy + y2)− (x+ y)xy ≥ (x − y)2 2 2 2 (x + y )(x − 2xy + y ) ≥ (x − y) (x + y )(x − y)2 − (x − y)2 ≥ 0 2 (x + y − 1)(x − y ) ≥ 0.

Ponieważ z założenia 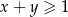x + y ≥ 1 otrzymana nierówność jest zawsze spełniona, więc wyjściowa nierówność też musiała być prawdziwa (bo przekształcaliśmy ją w sposób równoważny).

Sposób II

Zauważmy, że jeżeli 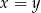x = y , to po obu stronach nierówności mamy 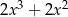2x 3 + 2x 2 . To jest przesłanka do tego, że w tej nierówności powinno dać się wyłączyć 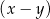(x − y) przed nawias. Próbujemy to zrobić.

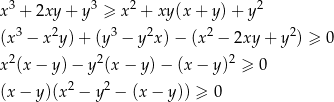
3 3 2 2 x + 2xy + y ≥ x + xy(x + y) + y (x3 − x2y) + (y3 − y2x) − (x2 − 2xy + y2) ≥ 0 2 2 2 x (x − y) − y (x − y )− (x − y ) ≥ 0 (x − y)(x2 − y2 − (x − y)) ≥ 0

Wyrażenie w drugim nawiasie jest równe

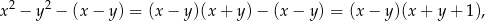
2 2 x − y − (x − y ) = (x − y)(x + y) − (x − y) = (x − y)(x+ y+ 1),

więc nierówność przyjmuje postać

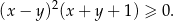
(x − y)2(x + y + 1) ≥ 0.

Ponieważ z założenia 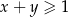x + y ≥ 1 otrzymana nierówność jest zawsze spełniona, więc wyjściowa nierówność też musiała być prawdziwa (bo przekształcaliśmy ją w sposób równoważny).

Wersja PDF