Zestaw użytkownika nr 3300_9810

sprawdzian z 1. semestru

Zadanie 1

(5 pkt)

Dla jakich wartości parametru 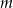równanie 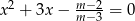2 m−-2 x + 3x − m− 3 = 0 ma dwa pierwiastki rzeczywiste? Wyznacz te wartości parametru 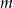, dla których suma sześcianów pierwiastków tego równania jest równa -9.

Zadanie 2

(5 pkt)

Naszkicuj wykres funkcji 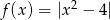2 f (x) = |x − 4| , a następnie określ liczbę rozwiązań równania 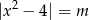|x2 − 4| = m w zależności od wartości parametru .

Zadanie 3

(5 pkt)

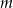Wyznacz wymiary prostokąta o obwodzie 36 cm, którego pole jest największe.

Zadanie 4

(5 pkt)

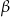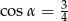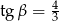Uzasadnij, że nie istnieje trójkąt prostokątny, w którym przeciwprostokątna ma długość 24, a kąty ostre i są takie, że cos α = 34 i tg β = 43 .

Zadanie 5

(5 pkt)

Podstawa 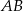trójkąta równoramiennego 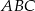ABC ma długość 8 oraz 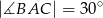|∡BAC | = 30∘ . Oblicz długość środkowej 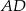tego trójkąta.

Zadanie 6

(5 pkt)

W jednokładności o środku 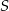i skali 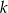obrazem okręgu o równaniu 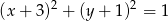(x + 3)2 + (y + 1)2 = 1 jest okrąg o równaniu 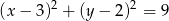(x− 3)2 + (y− 2)2 = 9 . Oblicz współrzędne środka 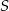jednokładności.

Zadanie 7

(5 pkt)

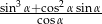Wyznacz miarę kąta ostrego , dla którego wyrażenie sin3α+cos2αsinα cosα przyjmuje wartość √ -- 3 .

Zadanie 8

(5 pkt)

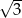Dane jest równanie 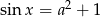2 sin x = a + 1 , z niewiadomą . Wyznacz wszystkie wartości parametru , dla których dane równanie nie ma rozwiązań.

Zadanie 9

(5 pkt)

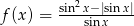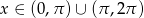Dana jest funkcja f określona wzorem sin2x−|sinx|- f(x) = sin x dla x ∈ (0,π) ∪ (π ,2 π) .

Naszkicuj wykres funkcji .
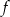Wyznacz miejsca zerowe funkcji .

Zadanie 10

(5 pkt)

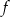Dany jest wykres funkcji logarytmicznej .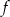

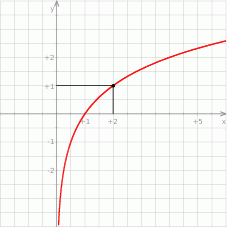
Wyznacz wzór funkcji .
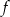Narysuj wykres funkcji .
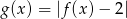Odczytaj z rysunku zbiór argumentów, dla których wartości funkcji 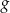są nie mniejsze od wartości funkcji .

Zadanie 11

(5 pkt)

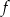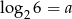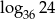Wiedząc, że log2 6 = a , wyznacz log 36 24 .

Zadanie 12

(5 pkt)

Wykaż, że jeżeli 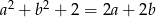2 2 a + b + 2 = 2a + 2b , to a = b = 1 .

Zadanie 13

(5 pkt)

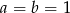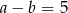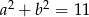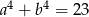Uzasadnij, że jeżeli a − b = 5 i 2 2 a + b = 11 , to 4 4 a + b = 23 .

Zadanie 14

(5 pkt)

Udowodnij, że dla dowolnych liczb dodatnich 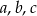a,b,c i 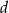prawdziwa jest nierówność

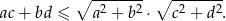
∘ ------- ∘ ------- ac + bd ≤ a2 + b2 ⋅ c2 + d2.

Zadanie 15

(5 pkt)

Liczby 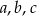a,b,c są trzema kolejnymi wyrazami ciągu arytmetycznego, a liczby 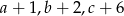a + 1,b + 2,c + 6 – trzema kolejnymi wyrazami ciągu geometrycznego. Znajdź liczby 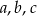a,b,c wiedząc, że ich suma jest równa 12.

Arkusz Wersja PDF