Zestaw użytkownika nr 7690_6378

Zestaw użytkownika
nr 7690_6378

Zadanie 1

(5 pkt)

Puszki z przecierem pomidorowym mają kształt walca o średnicy podstawy 4 cm oraz wysokości 3 cm. Puszki te mogą być na kilka sposobów zapakowane ciasno po 4 sztuki w prostopadłościenne tekturowe pudełka. Wybierz jeden z możliwych sposobów zapakowania puszek, zrób odręczny rysunek siatki odpowiedniego prostopadłościanu i podaj długości krawędzi tego prostopadłościanu.

Zadanie 2

(5 pkt)

Huta szkła produkuje kulki szklane o promieniu 5 cm. Do wysyłki będą one pakowane po 4 sztuki w sztywne pudełka w kształcie walca, którego wysokość wynosi 10 cm, a średnica 24 cm. Czy dobrze została dobrana średnica tych pudełek?

Zadanie 3

(5 pkt)

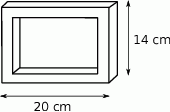
Wojtek wykonał prostokątną ramkę z drewnianych listewek, których przekrój poprzeczny jest kwadratem o boku 2 cm. Zewnętrzne wymiary ramki podane są na rysunku. Oblicz masę ramki, wiedząc, że 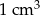1 cm 3 drewna, z którego ją wykonano, ma masę 0,8 g. Zapisz obliczenia.

Zadanie 4

(5 pkt)

Uzasadnij, że dwusieczne dwóch sąsiednich kątów równoległoboku przecinają się pod kątem prostym.

Zadanie 5

(1 pkt)

Do czterech naczyń 1, 2, 3 i 4 (patrz rysunek) o tej samej pojemności równej 300 ml wlano po 150 ml wody. W dwóch naczyniach wodę wlano dokładnie do połowy ich wysokości.

Które to naczynia?
A) 3 i 4 B) 1 i 3 C) 1 i 2 D) 2 i 4

Zadanie 6

(5 pkt)

Beczka ma pojemność 67,2 litra, dzbanek - 1,6 litra, a kubek ma pojemność 5 razy mniejszą niż dzbanek. Napełnienie dzbanka wodą z kranu trwa 20 s, pokonanie drogi od kranu do beczki trwa 10 s i tyle samo trwa powrót do kranu. Wylewanie wody z dzbanka trwa 5 s.

Ile czasu zajmie napełnienie beczki wodą za pomocą dzbanka?
Ile czasu zajęłoby napełnienie beczki wodą za pomocą kubka? Przyjmijmy, że dojście do beczki i powrót do kranu z kubkiem w ręku trwa tyle samo, co z dzbankiem.

W obu sytuacjach należy przyjąć, że na początku i na końcu stoimy przy beczce.

Zadanie 7

(5 pkt)

Oblicz objętość i pole powierzchni graniastosłupa, którego podstawą jest romb o przekątnych długości 6 cm i 8 cm, którego przekątna ściany bocznej tworzy z krawędzią podstawy kąt o mierze 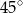45∘ .

Zadanie 8

(1 pkt)

Bryłę ułożono z jednakowych sześciennych klocków. Na rysunkach przedstawiony jest widok tej bryły z dwóch stron.

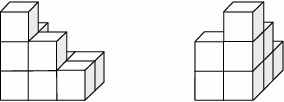
Z ilu klocków składa się ta bryła?
A) 8 B) 10 C) 9 D) 7

Zadanie 9

(5 pkt)

Każdy z dwóch jednakowych sześcianów o krawędzi 2 cm podzielono na mniejsze sześciany o krawędzi 1 cm. Czy z otrzymanych w ten sposób małych sześciennych kostek można ułożyć jeden pełny sześcian, tak by wszystkie kostki były wykorzystane? Wybierz odpowiedź TAK lub NIE i jej uzasadnienie wybrane spośród A, B, C, D.

TAK

NIE

A)	Liczba małych kostek nie jest podzielna przez 3.
B)	Liczba małych kostek jest potęgą liczby 2.
C)	Liczba małych kostek jest drugą potęgą liczby naturalnej.
D)	Liczba małych kostek nie jest trzecią potęgą liczby naturalnej.

Zadanie 10

(5 pkt)

Metalową kulę o promieniu 10 cm i stożek o średnicy 16 cm i wysokości 12cm przetopiono. Następnie z otrzymanego metalu wykonano walec o średnicy 8cm. Jaką wysokość ma ten walec?

Zadanie 11

(5 pkt)

Drwal miał ułożyć 46 okrągłych bali w stosy po 6 bali. Ile takich stosów (patrz rysunek) może ułożyć drwal?
Zapisz obliczenia i odpowiedź.

Zadanie 12

(5 pkt)

Suma wszystkich krawędzi ostrosłupa prawidłowego trójkątnego wynosi 72 cm. Oblicz długość krawędzi podstawy tego ostrosłupa, jeśli krawędź boczna ma długość 16 cm.

Zadanie 13

(5 pkt)

Rysunek przedstawia ostrosłup prosty.
Oceń, czy podane zdania są prawdziwe. Zaznacz TAK lub NIE.

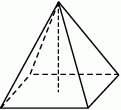
Ściany boczne ostrosłupa są trójkątami prostokątnymi.	TAK	NIE
Liczba wszystkich krawędzi ostrosłupa jest parzysta.	TAK	NIE
Wszystkie ściany boczne ostrosłupa mają wspólny wierzchołek.	TAK	NIE

Zadanie 14

(5 pkt)

Z czterech ołowianych sześcianów o przekątnej długości 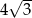√ -- 4 3 wykonano graniastosłup prawidłowy czworokątny o krawędzi podstawy długości 8. Oblicz długość przekątnej graniastosłupa.

Zadanie 15

(5 pkt)

W graniastosłupie prawidłowym czworokątnym powierzchnia boczna po rozwinięciu jest kwadratem o polu 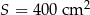S = 400 cm 2 . Oblicz objętość i pole powierzchni całkowitej tej bryły .

Zadanie 16

(5 pkt)

Oblicz pole powierzchni i objętość sześcianu, którego przekątna ma długość 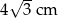√ -- 4 3 cm .

Zadanie 17

(5 pkt)

Maciek pływa w basenie o długości 25 m. W jednym końcu basenu głębokość wynosi 3 m, a w drugim 1,5 m. Kąt nachylenia dna basenu do powierzchni wody jest stały.

Czy Maciek ’ma grunt’ pod stopami w odległości 10 m od płytszego końca basenu? Przyjmij, że wzrost Maćka wynosi 180 cm, a basen jest całkowicie wypełniony wodą.
Oblicz pojemność basenu, w którym pływa Maciek. Szerokość basenu wynosi 10 m.

Zadanie 18

(1 pkt)

Siatka narysowanego graniastosłupa prostego składa się

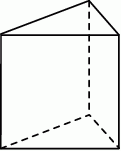
A) z 2 trójkątów i 2 prostokątów
B) z 3 trójkątów i 3 prostokątów
C) z 3 trójkątów i 2 prostokątów
D) z 2 trójkątów i 3 prostokątów

Zadanie 19

(3 pkt)

Z 36 sześcianów o krawędziach długości 1 zbudowano graniastosłup prawidłowy czworokątny. Które wymiary, z podanych w tabeli, może mieć ten graniastosłup?

I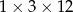
II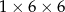
III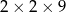
IV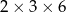
V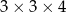

A) I, II i IV B) II, III i V C) III, IV i V D) I, II i III E) Wszystkie podane.

Zadanie 20

(5 pkt)

Długość promienia walca zmniejszono dziesięciokrotnie. Ile razy trzeba zwiększyć wysokość tego walca aby objętość się nie zmieniła?

Zadanie 21

(5 pkt)

Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni i objętość tej bryły.

Zadanie 22

(1 pkt)

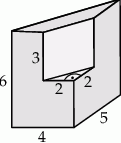
Długość przekątnej prostokąta przedstawionego na rysunku jest równa

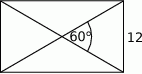
A) 12 B) 20 C) 24 D) 16

Zadanie 23

(5 pkt)

Ponumeruj poniższe czynności od 1 do 4 według kolejności prowadzącej do skonstruowania symetralnej odcinka .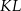
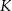. . . . . Kreślimy okręgi o promieniu i środkach w i .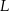
. . . . . Prowadzimy prostą przechodzącą przez punkty wspólne okręgów.
. . . . . Wybieramy odcinek większy od połowy długości odcinka .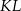
. . . . . Wyznaczamy punkty wspólne okręgów.

Zadanie 24

(5 pkt)

Czy kulę o objętości 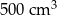3 50 0 cm można przełożyć przez otwór w kształcie kwadratu o boku 10 cm? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–D.

ponieważ

A)	średnica kuli jest mniejsza od przekątnej kwadratu.
B)	średnica kuli jest mniejsza od boku kwadratu.
C)	średnica kuli jest większa od przekątnej kwadratu.
D)	średnica kuli jest większa od boku kwadratu.

Zadanie 25

(5 pkt)

Oblicz objętość bryły, której kształt i wymiary przedstawiono na rysunku. Zapisz obliczenia.

Zadanie 26

(5 pkt)

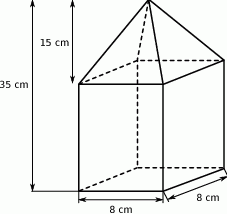
Piaskownica ma kształt prostopadłościanu o wymiarach 3 m na 3 m na 0,5 m. 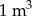1 m 3 piasku waży około 1,6 tony. Ile waży piasek wypełniający piaskownicę do jej wysokości?

Zadanie 27

(5 pkt)

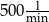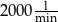Basen w najpłytszym miejscu ma 80 cm, a w najgłębszym 2,2 m głębokości. Jego długość wynosi 50 m, a szerokość 15 m. Jak długo będzie się on napełniał, jeśli woda wpada przez sześć kranów o wydajności 500--l- min i jeden o wydajności -l-- 20 00min ?

Zadanie 28

(5 pkt)

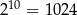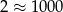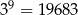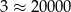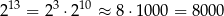Liczbę 10 2 = 1024 możemy przybliżyć tak: 2 ≈ 10 00 , a liczbę 9 3 = 19683 tak: 3 ≈ 2000 0 . To pozwala przybliżać inne liczby, na przykład 213 = 2 3 ⋅210 ≈ 8 ⋅1000 = 8000 .
Wykorzystując podane przybliżenia liczb 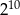210 oraz 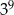, wybierz najlepsze przybliżenie liczb 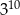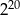10 3 , 20 2 oraz 9 6 .

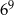Potęga	Propozycje przybliżeń
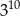	A) 30 000	B) 60 000	C) 200 000
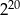	A) 2 000	B) 4 000	C) 1 000 000
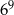	A) 15 000	B) 40 000	C) 10 000 000

Zadanie 29

(5 pkt)

Popatrz na kostkę przedstawioną na rysunku. Wiadomo, że na każdej ścianie narysowany jest odcinek oraz że odcinki na przeciwległych ścianach są równoległe. Narysuj siatkę z której można skleić tę kostkę. Na każdej ścianie narysuj odpowiedni odcinek.

Zadanie 30

(5 pkt)

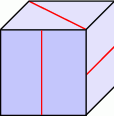
Z jednakowych sześciennych kostek, których krawędź ma długość 1, sklejono bryłę przedstawioną na rysunku.

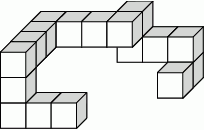
Ile kostek należy dokleić do tej bryły, aby otrzymać wypełniony kostkami sześcian?

Zadanie 31

(5 pkt)

Prostopadłościenne kartoniki z sokiem o pojemności 125 ml każdy umieszczono w 3 kartonach, których podstawą jest prostokąt o obwodzie 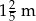1 25 m , długości 35 cm. Wysokość tego kartonu jest o 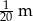120 m mniejsza od szerokości podstawy.

Ile kartoników z sokiem było w każdym kartonie?
Ile litrów napoju było w tych kartonach razem?

Zadanie 32

(5 pkt)

W prostopadłościanie pola trzech ścian o wspólnym wierzchołku są równe 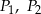P 1, P2 i 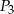. Oblicz objętość tego prostopadłościanu.

Zadanie 33

(5 pkt)

Oblicz objętość kuli wiedząc że jej pole powierzchni jest równe 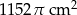2 1152π cm .

Zadanie 34

(5 pkt)

Wodę wypartą przez kamień wlano do prostopadłościennego naczynia o wymiarach 7 cm, 5 cm i 15 cm. Woda wypełniła 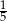pojemności tego naczynia. Jaką objętość ma kamień?

Zadanie 35

(5 pkt)

Deska dębowa ma 3 m długości, 25 cm szerokości i 3 cm grubości. 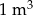3 1 m drewna dębowego waży 660 kg. Ile kilogramów waży ta deska?

Zadanie 36

(5 pkt)

O ile procent należy wydłużyć krawędź sześcianu, aby jego pole powierzchni wzrosło o 21%?

Zadanie 37

(5 pkt)

Ile ścian bocznych ma graniastosłup o 14 wierzchołkach?

Zadanie 38

(5 pkt)

Poczta przyjmuje do wysłania tylko te paczki, których wymiary spełniają określone warunki. Jeśli paczka ma kształt prostopadłościanu, to spełnione muszą być następujące trzy warunki:
a) najdłuższa krawędź (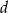) tego prostopadłościanu nie może przekraczać 150 cm
b) suma długości 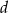i obwodu ściany ograniczonej krótszymi krawędziami nie może przekraczać 300 cm
c) jedna ze ścian paczki (przeznaczona do naklejenia adresu) musi mieć wymiary co najmniej 14 cm na 9 cm.

Przygotowano paczki o wymiarach
I: 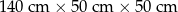140 cm × 50 cm × 50 cm
II: 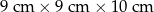9 cm × 9 cm × 10 cm
III: 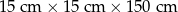15 cm × 1 5 cm × 150 cm
Uzupełnij tabelę

Nr paczki	Czy paczka zostanie przyjęta do wysłania? Wpisz TAK lub NIE	Jeśli paczka nie zostanie przyjęta do wysłania, podaj warunek, który nie został spełniony. Wpisz literę a, b lub c
I
II
III

Zadanie 39

(5 pkt)

Wysokość prostopadłościanu o podstawie kwadratowej jest dwa razy dłuższa od krawędzi podstawy. Objętość prostopadłościanu jest równa 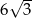√ -- 6 3 . Wyznacz pole powierzchni całkowitej tego prostopadłościanu.

Zadanie 40

(5 pkt)

Graniastosłup prawidłowy czworokątny o krawędzi 4 cm i wysokości 3 cm przecięto płaszczyzną, która zawiera przekątne przeciwległych ścian bocznych. Jakie pole ma ten przekrój?

Rozwiąż on-line Arkusz Wersja PDF