Zadanie nr 8510933
Punkt 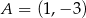 jest wierzchołkiem trójkąta
jest wierzchołkiem trójkąta 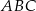 , w którym
, w którym 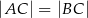 . Punkt
. Punkt 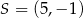 jest środkiem odcinka
jest środkiem odcinka 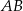 . Wierzchołek
. Wierzchołek 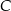 tego trójkąta leży na prostej o równaniu
tego trójkąta leży na prostej o równaniu 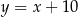 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 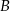 i
i 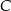 tego trójkąta.
tego trójkąta.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
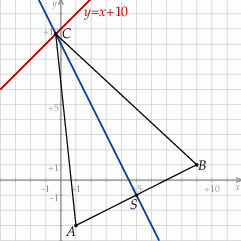
Wiemy, że 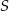 jest środkiem odcinka
jest środkiem odcinka 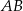 , więc łatwo obliczyć współrzędne wierzchołka
, więc łatwo obliczyć współrzędne wierzchołka 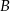 .
.
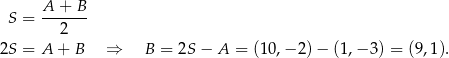
Współrzędne punktu 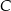 wyznaczymy na dwa sposoby.
wyznaczymy na dwa sposoby.
Sposób I
Wiemy, że punkt 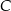 leży na prostej
leży na prostej 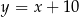 , więc ma współrzędne postaci
, więc ma współrzędne postaci 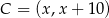 . Wiemy też, że trójkąt
. Wiemy też, że trójkąt 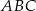 jest równoramienny, więc
jest równoramienny, więc
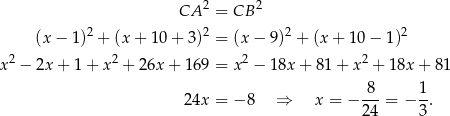
Stąd 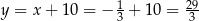 i
i 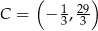 .
.
Sposób II
Punkt 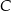 jest punktem wspólnym danej prostej
jest punktem wspólnym danej prostej 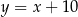 i symetralnej boku
i symetralnej boku 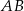 . Napiszmy równanie tej symetralnej. Można to zrobić na wiele sposobów, my skorzystamy ze wzoru na równanie prostej przechodzącej przez punkt
. Napiszmy równanie tej symetralnej. Można to zrobić na wiele sposobów, my skorzystamy ze wzoru na równanie prostej przechodzącej przez punkt 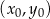 i prostopadłej do wektora
i prostopadłej do wektora ![→v = [p,q]](https://img.zadania.info/zad/8510933/HzadR17x.gif) .
.
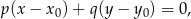
W naszej sytuacji mamy ![→ −→ v = AB = [8,4]](https://img.zadania.info/zad/8510933/HzadR19x.gif) oraz
oraz 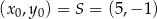 . Zatem symetralna odcinka
. Zatem symetralna odcinka 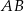 ma równanie
ma równanie
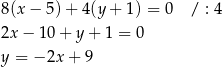
Pozostało teraz znaleźć punkt wspólny tej prostej z podaną prostą 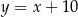 . Podstawiamy
. Podstawiamy 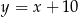 do powyższego równania.
do powyższego równania.
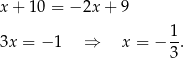
Stąd 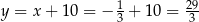 i
i 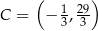 .
.
Odpowiedź: 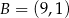 ,
,