Kąt  jest ostry i
jest ostry i 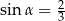 . Wtedy
. Wtedy 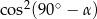 jest równy
jest równy
A)  B)
B)  C)
C)  D)
D) 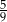
/Szkoła średnia
Funkcja 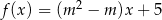 jest funkcją stałą. Wynika stąd, że
jest funkcją stałą. Wynika stąd, że
A) 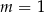 B)
B) 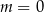 C)
C) 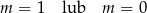 D)
D) 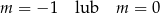
Wskaż 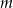 , dla którego funkcja liniowa określona wzorem
, dla którego funkcja liniowa określona wzorem 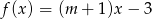 jest stała.
jest stała.
A) 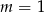 B)
B) 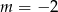 C)
C) 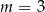 D)
D) 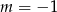
Wskaż 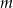 , dla którego funkcja liniowa określona wzorem
, dla którego funkcja liniowa określona wzorem 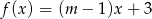 jest stała.
jest stała.
A) 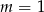 B)
B) 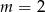 C)
C) 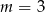 D)
D) 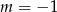
Funkcja 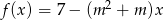 jest funkcją stałą. Wynika stąd, że
jest funkcją stałą. Wynika stąd, że
A) 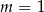 B)
B) 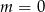 C)
C) 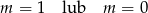 D)
D) 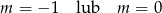
Funkcja 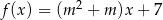 jest funkcją stałą. Wynika stąd, że
jest funkcją stałą. Wynika stąd, że
A) 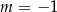 B)
B) 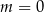 C)
C) 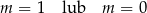 D)
D) 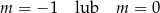
Funkcja 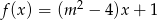 jest funkcją stałą. Wynika stąd, że
jest funkcją stałą. Wynika stąd, że
A) 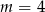 B)
B) 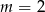 C)
C) 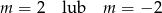 D)
D) 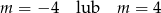
Rozwiąż równanie 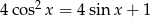 w przedziale
w przedziale 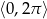 .
.
Wyznacz wszystkie rozwiązania równania 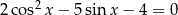 należące do przedziału
należące do przedziału 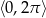 .
.
Rozwiąż równanie 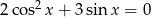 w przedziale
w przedziale 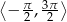 .
.
Wyznacz wszystkie rozwiązania równania 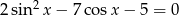 należące do przedziału
należące do przedziału 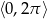 .
.
Rozwiąż równanie 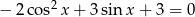 w przedziale
w przedziale 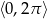 .
.
Dany jest wykres funkcji logarytmicznej 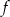 .
.
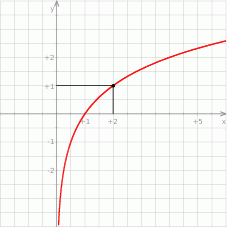
- Wyznacz wzór funkcji
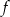 .
. - Narysuj wykres funkcji
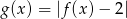 .
. - Odczytaj z rysunku zbiór argumentów, dla których wartości funkcji
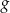 są nie mniejsze od wartości funkcji
są nie mniejsze od wartości funkcji 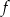 .
.
Zbadaj dla jakich wartości parametru 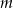 punkt przecięcia się prostych
punkt przecięcia się prostych 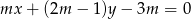 i
i 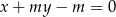 należy do prostokąta o wierzchołkach
należy do prostokąta o wierzchołkach 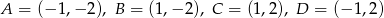 ?
?
Wskaż nierówność, którą spełnia liczba 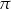 .
.
A) 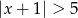 B)
B) 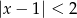 C)
C) 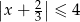 D)
D) 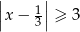
Wskaż nierówność, którą spełnia liczba 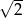 .
.
A) 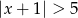 B)
B) 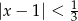 C)
C) 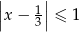 D)
D) 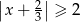
Wskaż nierówność, którą spełnia liczba 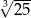 .
.
A) 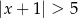 B)
B) 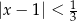 C)
C) 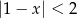 D)
D) 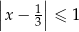
Wskaż nierówność, którą spełnia liczba 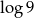 .
.
A) 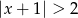 B)
B) 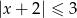 C)
C) 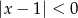 D)
D) 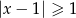
Podstawą graniastosłupa prawidłowego jest trójkąt, w którym długość wysokości wynosi 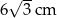 . Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt o mierze
. Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt o mierze 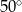 . Oblicz pole powierzchni całkowitej i objętość graniastosłupa. Wynik podaj z dokładnością do 1 cm.
. Oblicz pole powierzchni całkowitej i objętość graniastosłupa. Wynik podaj z dokładnością do 1 cm.
Cenę pewnego towaru obniżono o 25%. O ile procent należy podnieść obecną cenę tego towaru, aby otrzymać cenę początkową?
A) o 20% B) o 33,(3)% C) o 15,(2)% D) o 22%
Cenę pewnego towaru obniżono o 20%. O ile procent należy podnieść obecną cenę tego towaru, aby otrzymać cenę początkową?
A) o 20% B) o 33,(3)% C) o 25% D) o 30%
Cenę  pewnego towaru obniżono o 36% i otrzymano cenę
pewnego towaru obniżono o 36% i otrzymano cenę 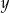 . Aby przywrócić cenę
. Aby przywrócić cenę  , nową cenę
, nową cenę 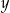 należy podnieść o
należy podnieść o
A) o 64% B) o 60% C) o 36% D) o 56,25%
Cenę  pewnego towaru obniżono o 20% i otrzymano cenę
pewnego towaru obniżono o 20% i otrzymano cenę 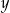 . Aby przywrócić cenę
. Aby przywrócić cenę  , nową cenę
, nową cenę 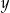 należy podnieść o
należy podnieść o
A) o 25% B) o 20% C) o 15% D) o 12%
Wyrażenie 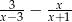 zapisz w postaci ilorazu dwóch wielomianów.
zapisz w postaci ilorazu dwóch wielomianów.
Na ile sposobów można rozmieścić sześć ponumerowanych kul w pięciu ponumerowanych szufladach tak, aby w każdej szufladzie była przynajmniej jedna kula.
Pięć ponumerowanych kul rozmieszczamy losowo w czterech ponumerowanych szufladach. Oblicz ile jest możliwości takiego rozmieszczenia kul, aby dokładnie dwie szuflady były puste.
Na ile sposobów można rozmieścić pięć ponumerowanych kul w czterech ponumerowanych szufladach tak, aby w każdej szufladzie była przynajmniej jedna kula.
Oblicz pole trójkąta ograniczonego prostą 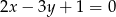 i osiami układu współrzędnych.
i osiami układu współrzędnych.
Wyznacz równanie okręgu symetrycznego do okręgu 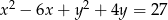 względem prostej
względem prostej 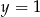 .
.
Cenę nart obniżono latem o 20%, a potem jeszcze o 15%. Po tych dwóch obniżkach narty kosztowały 705 zł i 50 gr. Wynika z tego, że pierwotna cena nart to
A) 952,42 zł B) 980 zł C) 1037,5 zł D) 1100 zł
Cenę aparatu fotograficznego obniżono o 15%, a następnie – o 20% w odniesieniu do ceny obowiązującej w danym momencie. Po tych dwóch obniżkach aparat kosztuje 340 zł. Przed obiema obniżkami cena tego aparatu była równa
A) 500 zł B) 425 zł C) 400 zł D) 375 zł
Cenę płetw obniżono zimą o 14%, a potem jeszcze o 20%. Po tych dwóch obniżkach płetwy kosztowały 242 zł i 52 gr. Wynika z tego, że pierwotna cena płetw to
A) 331,77 zł B) 352,5 zł C) 347 zł D) 395 zł
Cenę pontonu obniżono zimą o 15%, a potem jeszcze o 25%. Po tych dwóch obniżkach ponton kosztował 1912 zł i 50 gr. Wynika z tego, że pierwotna cena pontonu to
A) 3000 zł B) 2749,22 zł C) 2974,22 zł D) 2000 zł
Punkty 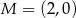 i
i 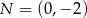 są punktami styczności okręgu z osiami układu współrzędnych. Jakie współrzędne ma środek tego okręgu?
są punktami styczności okręgu z osiami układu współrzędnych. Jakie współrzędne ma środek tego okręgu?
A) 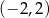 B)
B) 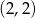 C)
C) 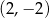 D)
D) 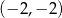
Punkty 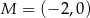 i
i 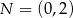 są punktami styczności okręgu z osiami układu współrzędnych. Jakie współrzędne ma środek tego okręgu?
są punktami styczności okręgu z osiami układu współrzędnych. Jakie współrzędne ma środek tego okręgu?
A) 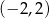 B)
B) 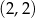 C)
C) 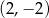 D)
D) 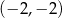
Podaj przykład liczb całkowitych dodatnich, spełniających nierówność 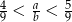 .
.
Podaj przykład liczb całkowitych dodatnich, spełniających nierówność 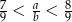 .
.
Podaj przykład liczb całkowitych dodatnich  i
i 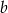 , spełniających nierówność
, spełniających nierówność 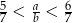 .
.
Podaj przykład liczb całkowitych 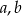 , dla których prawdziwa jest nierówność podwójna:
, dla których prawdziwa jest nierówność podwójna:
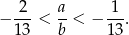
Dana jest funkcja 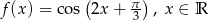 .
.
- Narysuj wykres funkcji
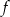 dla
dla 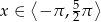 .
. - Rozwiąż równanie:
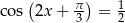 , dla
, dla 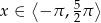 .
.
Pierwszy wyraz nieskończonego ciągu geometrycznego 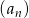 jest równy
jest równy 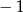 . Wyraz drugi, trzeci i czwarty spełniają warunek
. Wyraz drugi, trzeci i czwarty spełniają warunek 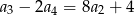 .
.
- Oblicz iloraz ciągu
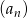 .
. - Określ, czy ciąg
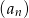 jest rosnący, czy malejący.
jest rosnący, czy malejący.
W ciągu arytmetycznym 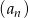 , określonym dla
, określonym dla 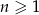 , dane są: wyraz
, dane są: wyraz 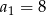 i suma trzech początkowych wyrazów tego ciągu
i suma trzech początkowych wyrazów tego ciągu 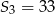 . Oblicz różnicę
. Oblicz różnicę 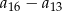 .
.
W ciągu arytmetycznym 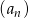 , określonym dla
, określonym dla 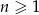 , dane są: wyraz
, dane są: wyraz 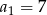 i suma czterech początkowych wyrazów tego ciągu
i suma czterech początkowych wyrazów tego ciągu 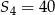 . Oblicz różnicę
. Oblicz różnicę 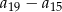 .
.
Wykaż, że jeżeli wielomian 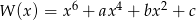 jest podzielny przez trójmian
jest podzielny przez trójmian 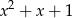 , to jest również podzielny przez trójmian
, to jest również podzielny przez trójmian 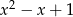 .
.
Wielomian 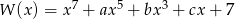 jest podzielny przez wielomian
jest podzielny przez wielomian 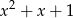 . Wyznacz resztę z dzielenia wielomianu
. Wyznacz resztę z dzielenia wielomianu 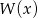 przez wielomian
przez wielomian 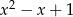 .
.
Tworząca stożka jest nachylona do podstawy pod kątem  . Kula opisana na tym stożku ma promień
. Kula opisana na tym stożku ma promień 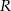 . Oblicz pole powierzchni całkowitej tego stożka.
. Oblicz pole powierzchni całkowitej tego stożka.

