W trójkącie jeden z kątów jest o 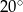 większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
A) 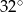 B)
B) 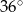 C)
C) 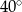 D)
D) 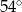
/Szkoła średnia
W trójkącie miary kątów są równe:  ,
, 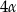 ,
, 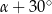 . Miara największego kąta tego trójkąta jest równa
. Miara największego kąta tego trójkąta jest równa
A) 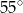 B)
B) 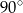 C)
C) 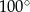 D)
D) 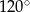
W trójkącie jeden z kątów jest o 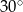 większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
A) 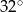 B)
B) 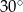 C)
C) 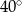 D)
D) 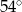
Jeden z kątów trójkąta jest trzy razy większy od drugiego. Miara trzeciego kąta jest o 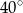 większa od miary najmniejszego kąta w tym trójkącie. Miary kątów tego trójkąta są równe
większa od miary najmniejszego kąta w tym trójkącie. Miary kątów tego trójkąta są równe
A) 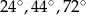 B)
B) 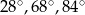 C)
C) 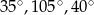 D)
D) 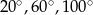
W trójkącie jeden z kątów jest o 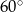 większy od najmniejszego, a trzeci kąt jest czterokrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
większy od najmniejszego, a trzeci kąt jest czterokrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
A) 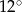 B)
B) 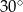 C)
C) 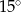 D)
D) 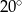
W trapezie równoramiennym krótsza podstawa i ramię mają taką samą długość. Przekątna trapezu tworzy z jednym z ramion kąt prosty. Oblicz miary kątów tego trapezu.
W klasie jest cztery razy więcej chłopców niż dziewcząt. Ile procent wszystkich uczniów tej klasy stanowią dziewczęta?
A) 4% B) 5% C) 20% D) 25%
W loterii fantowej jest 9 razy więcej losów przegrywających niż wygrywających. Ile procent wszystkich losów w tej loterii stanowią losy wygrywające?
A) 1% B) 11% C) 10% D) 90%
Liczby 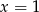 i
i 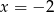 są pierwiastkami wielomianu
są pierwiastkami wielomianu 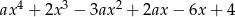 . Wiedząc, że wielomian ten jest kwadratem wielomianu stopnia 2, oblicz
. Wiedząc, że wielomian ten jest kwadratem wielomianu stopnia 2, oblicz  .
.
W koszu znajdują się owoce: 12 jabłek i 8 pomarańczy. Wyjmujemy kolejno trzy owoce, nie odkładając ich do kosza. Jakie jest prawdopodobieństwo, że wylosujemy dokładnie dwie pomarańcze.
W pudełku jest 7 kul białych i 3 czarne. Doświadczenie polega na wylosowaniu 3 kul. Jakie jest prawdopodobieństwo wylosowania co najwyżej dwóch kul białych?
Ze zbioru liczb 3, 4, 1, 5, 1, 3, 1 usunięto jedną liczbę w ten sposób, że mediana tego zbioru liczb nie uległa zmianie. Usunięta liczba to
A) 1 B) 3 C) 4 D) 5
Równanie 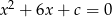 nie ma rozwiązania, gdy
nie ma rozwiązania, gdy
A) 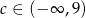 B)
B) 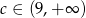 C)
C) 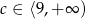 D)
D) 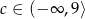
Równanie 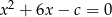 nie ma rozwiązania, gdy
nie ma rozwiązania, gdy
A) 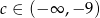 B)
B) 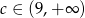 C)
C) 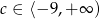 D)
D) 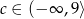
Równanie 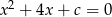 nie ma rozwiązania, gdy
nie ma rozwiązania, gdy
A) 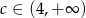 B)
B) 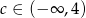 C)
C) 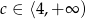 D)
D) 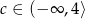
W równoległoboku 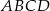 przekątne przecinają się w punkcie
przekątne przecinają się w punkcie 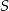 . Niech
. Niech 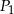 oznacza pole trójkąta
oznacza pole trójkąta 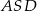 , natomiast
, natomiast 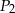 oznacza pole trójkąta
oznacza pole trójkąta 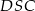 . Wówczas:
. Wówczas:
A) 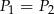 B)
B) 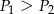 C)
C) 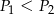 D)
D) 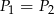 tylko wtedy, gdy
tylko wtedy, gdy 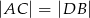
W równoległoboku 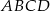 przekątne przecinają się w punkcie
przekątne przecinają się w punkcie 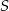 . Niech
. Niech 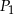 oznacza pole trójkąta
oznacza pole trójkąta 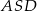 , natomiast
, natomiast 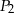 oznacza pole trójkąta
oznacza pole trójkąta 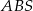 . Wówczas:
. Wówczas:
A) 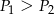 B)
B) 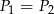 C)
C) 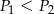 D)
D) 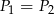 tylko wtedy, gdy
tylko wtedy, gdy 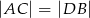
Cięciwy 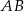 i
i 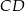 okręgu o środku
okręgu o środku 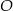 przecinają się w punkcie
przecinają się w punkcie 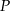 i tworzą trójkąty
i tworzą trójkąty 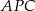 i
i 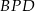 .
.
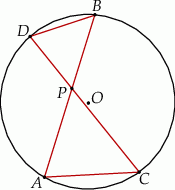
Trójkąty 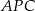 i
i 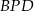 są
są
| A) podobne, | B) przystające, |
ponieważ trójkąty te mają równe
| 1) pola, | 2) miary kątów, | 3) długości boków, |
Rzucamy 3 razy kostką do gry. Oblicz prawdopodobieństwo, że kolejno otrzymane liczby utworzą ciąg arytmetyczny.
Rzucamy 3 razy kostką do gry. Oblicz prawdopodobieństwo, że kolejno otrzymane liczby utworzą ciąg geometryczny.
Gdy przesuniemy wykres funkcji 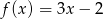 o 3 jednostki w prawo i 2 jednostki w górę, to otrzymamy wykres funkcji opisanej wzorem
o 3 jednostki w prawo i 2 jednostki w górę, to otrzymamy wykres funkcji opisanej wzorem
A) 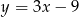 B)
B) 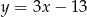 C)
C) 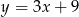 D)
D) 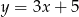
Aby otrzymać wykres funkcji 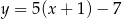 , należało wykres funkcji
, należało wykres funkcji 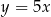 przesunąć
przesunąć
A) o 1 jednostkę w lewo i 7 ku dołowi B) o 1 jednostkę w prawo i 7 ku górze
C) o 1 jednostkę w prawo i 7 ku dołowi D) o 1 jednostkę w lewo i 7 ku górze
Gdy przesuniemy wykres funkcji 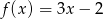 o 3 jednostki w lewo i 2 jednostki w dół, to otrzymamy wykres funkcji opisanej wzorem
o 3 jednostki w lewo i 2 jednostki w dół, to otrzymamy wykres funkcji opisanej wzorem
A) 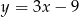 B)
B) 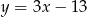 C)
C) 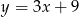 D)
D) 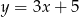
Punkty 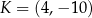 i
i 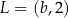 są końcami odcinka
są końcami odcinka 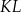 . Pierwsza współrzędna środka odcinka
. Pierwsza współrzędna środka odcinka 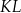 jest równa
jest równa 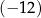 . Wynika stąd, że
. Wynika stąd, że
A) 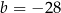 B)
B) 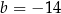 C)
C) 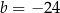 D)
D) 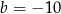
Tabela przedstawia pewne dane i ich liczebność
| Wartość danej | -4 | 2 | 4 | 7 | 20 |
| Liczebność | 7 | 2 | 3 | 6 | 2 |
- Oblicz średnią arytmetyczną tych danych.
- Podaj medianę.
- Oblicz odchylenie standardowe.
Wykres funkcji homograficznej 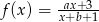 można otrzymać przesuwając wykres funkcji
można otrzymać przesuwając wykres funkcji 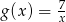 , a dziedzina funkcji
, a dziedzina funkcji 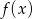 jest tym samym zbiorem co jej zbiór wartości. Wyznacz współczynniki
jest tym samym zbiorem co jej zbiór wartości. Wyznacz współczynniki  i
i 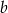 .
.
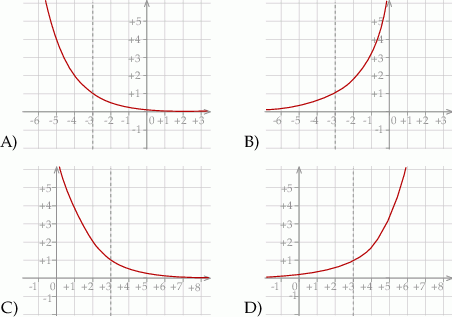
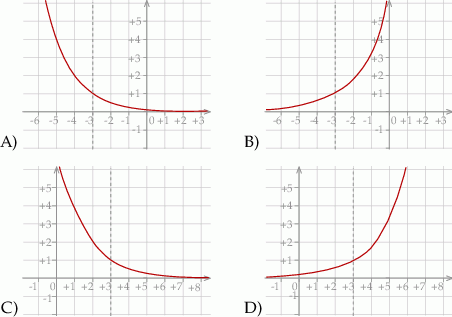
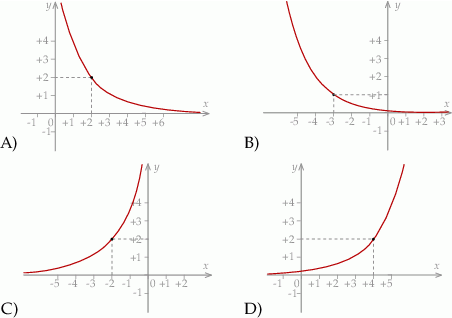
Wykres funkcji 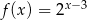 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
Wykres funkcji 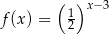 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
Wykres funkcji 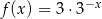 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
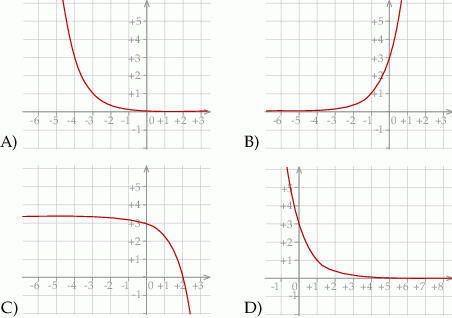
Wykres funkcji 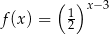 przedstawiony jest na rysunku
przedstawiony jest na rysunku
Wykaż, że nie istnieje kąt  , taki, że
, taki, że 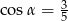 i
i 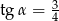 .
.
Liczba 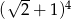 jest większa od liczby
jest większa od liczby 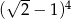 o
o
A) 2 B) 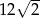 C)
C) 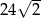 D)
D) 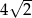
Pole powierzchni bocznej walca wynosi 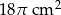 . Wysokość walca jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego walca jest równe
. Wysokość walca jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego walca jest równe
A) 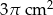 B)
B) 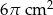 C)
C) 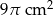 D)
D) 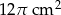
Niech 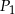 będzie prostokątem o polu
będzie prostokątem o polu 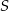 i stosunku długości boków równym 3:2. Konstruujemy kolejno prostokąty
i stosunku długości boków równym 3:2. Konstruujemy kolejno prostokąty 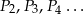 podobne do prostokąta
podobne do prostokąta 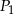 takie, że dłuższy bok kolejnego prostokąta jest równy krótszemu bokowi poprzedniego prostokąta. Oblicz sumę pól prostokątów
takie, że dłuższy bok kolejnego prostokąta jest równy krótszemu bokowi poprzedniego prostokąta. Oblicz sumę pól prostokątów 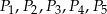 .
.
Odcinek 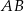 jest średnicą okręgu (rysunek).
jest średnicą okręgu (rysunek).
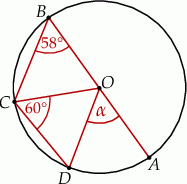
Miara kąta  jest równa
jest równa
A) 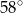 B)
B) 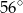 C)
C) 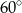 D)
D)