Zadanie nr 1021234
Przez punkt 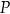 krawędzi bocznej
krawędzi bocznej 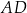 graniastosłupa prawidłowego trójkątnego
graniastosłupa prawidłowego trójkątnego 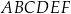 o krawędzi podstawy równej
o krawędzi podstawy równej  poprowadzono dwie płaszczyzny. Jedna przechodzi przez przeciwległą krawędź dolnej podstawy i jest nachylona do tej podstawy pod kątem
poprowadzono dwie płaszczyzny. Jedna przechodzi przez przeciwległą krawędź dolnej podstawy i jest nachylona do tej podstawy pod kątem  , a druga przechodzi przez przeciwległą krawędź górnej podstawy i jest nachylona do tej podstawy pod kątem
, a druga przechodzi przez przeciwległą krawędź górnej podstawy i jest nachylona do tej podstawy pod kątem 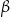 (zobacz rysunek).
(zobacz rysunek).
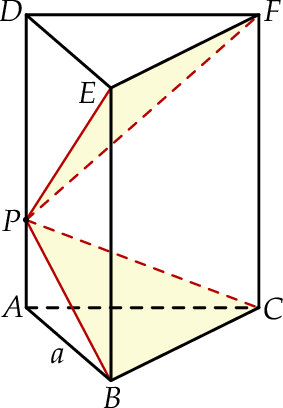
Udowodnij, że objętość ostrosłupa 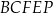 jest równa
jest równa
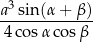
Rozwiązanie
Niech 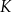 i
i 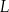 będą środkami odpowiednio krawędzi
będą środkami odpowiednio krawędzi 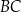 i
i 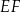 oraz oznaczmy
oraz oznaczmy 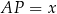 ,
, 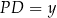 .
.
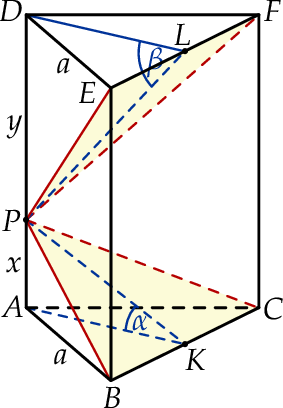
Przy tych oznaczeniach podane kąty nachylenia płaszczyzn 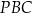 i
i 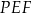 do płaszczyzn podstaw graniastosłupa są odpowiednio równe
do płaszczyzn podstaw graniastosłupa są odpowiednio równe
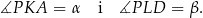
Z trójkątów prostokątnych 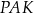 i
i 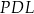 mamy
mamy
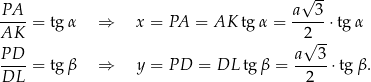
Objętość ostrosłupa 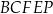 jest więc równa
jest więc równa