Zadanie nr 9203435
Po torze wodnym o długości 10 km pływają w kółko dwie łodzie motorowe, przy czym druga z nich płynie z prędkością o 5 km/h większą od prędkości pierwszej łodzi. Łodzie te wystartowały z tego samego punktu i ponownie spotkały się, gdy pierwsza z łodzi wykonała pełne 3 okrążenia toru. Oblicz średnie prędkości obu łodzi.
Rozwiązanie
Zauważmy, że czas jaki upływa między kolejnymi spotkaniami łodzi to dokładnie czas, w którym druga łódź przepłynie o 10 km więcej od pierwszej łodzi. Jeżeli więc oznaczymy przez  prędkość pierwszej łodzi to mamy układ równań
prędkość pierwszej łodzi to mamy układ równań
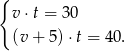
Przekształcamy drugie równanie korzystając z pierwszego.
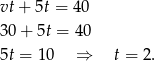
Zatem 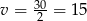 i prędkość drugiej łodzi wynosi
i prędkość drugiej łodzi wynosi 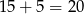 .
.
Odpowiedź: 15 km/h i 20 km/h

