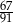Zadanie nr 9206513
Spośród wyrazów skończonego ciągu arytmetycznego 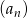 danego wzorem
danego wzorem 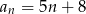 , gdzie
, gdzie 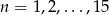 wybieramy losowo 3. Oblicz prawdopodobieństwo, że iloczyn wybranych liczb jest podzielny przez 3.
wybieramy losowo 3. Oblicz prawdopodobieństwo, że iloczyn wybranych liczb jest podzielny przez 3.
Rozwiązanie
Losujemy ze zbioru mającego 15 elementów, czyli
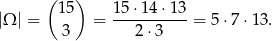
Zanim policzymy ile jest zdarzeń sprzyjających, sprawdźmy ile wyrazów podanego ciągu dzieli się przez 3. Wypiszmy kilka pierwszych wyrazów
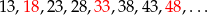
Zaczyna być widać, że co trzeci wyraz ciągu jest podzielny przez 3. Jeżeli ktoś jest pracowity to może wypisać 15 wyrazów ciągu i sprawdzić, że tak jest (i jednocześnie policzyć ile ich jest). Zamiast tego możemy też zauważyć, że jeżeli  dzieli się przez 3, czyli
dzieli się przez 3, czyli 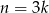 dla pewnego
dla pewnego 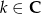 , to
, to
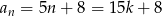
nie jest podzielne przez 3. Jeżeli 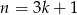 dla pewnego
dla pewnego 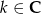 (czyli
(czyli  daje resztę 1 z dzielenia przez 3) to
daje resztę 1 z dzielenia przez 3) to
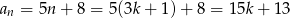
i ponownie otrzymujemy liczbę, która nie jest podzielna przez 3. Jeżeli w końcu 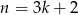 dla pewnego
dla pewnego 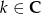 (
( daje resztę 2 z dzielenia przez 3) to
daje resztę 2 z dzielenia przez 3) to
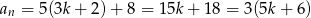
jest liczbą podzielną przez 3.
W takim razie wyrazy ciągu 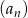 , które dzielą się przez 3 to
, które dzielą się przez 3 to
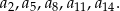
Jak widać jest ich 5.
Sposób I
Zamiast liczyć prawdopodobieństwo 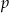 otrzymania iloczynu podzielnego przez 3, policzmy prawdopodobieństwo
otrzymania iloczynu podzielnego przez 3, policzmy prawdopodobieństwo 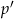 otrzymania iloczyny, który nie dzieli się przez 3. W takim zdarzeniu żadna z wylosowanych liczb nie może dzielić się przez 3, czyli jest
otrzymania iloczyny, który nie dzieli się przez 3. W takim zdarzeniu żadna z wylosowanych liczb nie może dzielić się przez 3, czyli jest
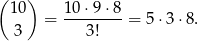
Mamy więc
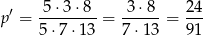
oraz
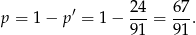
Sposób II
Liczymy liczbę zdarzeń sprzyjających. Są one trzech rodzajów:
– wszystkie trzy wylosowane liczby są podzielne przez 3, jest
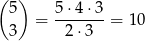
tego typu zdarzeń;
– dwie spośród wylosowanych liczb są podzielne przez 3, jest
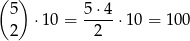
takich zdarzeń (do dwóch liczb podzielnych przez 3 dobieramy jedną, która nie jest podzielna);
– dokładnie jedna z wylosowanych liczb dzieli się przez 3, jest
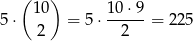
takich zdarzeń.
W sumie jest więc
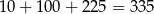
zdarzeń sprzyjających i prawdopodobieństwo wynosi
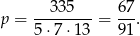
Odpowiedź: