/Szkoła średnia

Zadanie nr 9207274

Dodaj do ulubionych
Dodaj do rozwiązanych

Firma obuwnicza otrzymała zamówienie na wykonanie 720 par butów. Aby zrealizować zamówienie na czas, postanowiono wykonywać dziennie jednakową liczbę par butów. Po wykonaniu 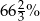6623 % zamówienia usprawniono produkcję tak, że dzienna produkcja wzrosła o 4 pary, zaś zamówienie zrealizowano o 5 dni wcześniej. W ciągu ilu dni planowano wykonać zamówienie?

Rozwiązanie

Oznaczmy przez 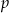p liczbę par butów jaką początkowo planowano robić dziennie oraz przez 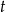t liczbę dni jaką przeznaczono na realizację zamówienia. Zatem

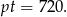
pt = 720.

Zmiana w produkcji nastąpiła po wykonaniu 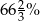66 2% 3 zamówienia, czyli po zrobieniu

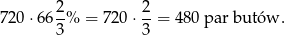
2- 2- 7 20⋅ 663% = 720⋅ 3 = 48 0 par but ów .

Wykonanie tej liczby par butów trwało

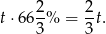
2- 2- t⋅66 3% = 3 t.

Zatem pozostało do zrobienia jeszcze 240 par butów, w planowanym czasie t3 dni.

Wiemy jednak, że zmieniono produkcję i produkowano dziennie 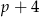p+ 4 par butów. Dzięki temu produkcja trwała jeszcze 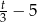t 3 − 5 dni. Otrzymujemy zatem układ równań

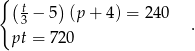
{ ( ) t3 − 5 (p + 4 ) = 240 pt = 720 .

Z drugiego równania mamy

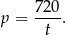
72 0 p = --t-.

Podstawiamy do pierwszego równania i otrzymujemy

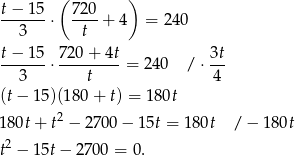
( ) t−--15 720- 3 ⋅ t + 4 = 24 0 t−--15 ⋅ 720-+-4t-= 240 / ⋅ 3t 3 t 4 (t− 1 5)(180 + t) = 180t 2 180t + t − 2 700− 15t = 180t / − 180t t2 − 1 5t− 27 00 = 0.

Liczymy 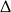Δ -ę i wyznaczamy pierwiastki

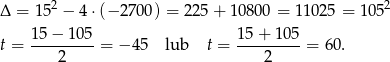
Δ = 152 − 4 ⋅(− 2700) = 2 25+ 10800 = 1 1025 = 1 052 1-5−-1-05 15+--105- t = 2 = − 45 lub t = 2 = 60.

Pierwiastek ujemny odrzucamy i otrzymujemy, że początkowo planowano wykonać zamówienie w ciągu 60 dni.  
Odpowiedź: 60 dni

Wersja PDF