Zadanie nr 9272500
Dane jest równanie kwadratowe 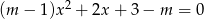 z niewiadomą
z niewiadomą  i parametrem
i parametrem 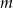 .
.
- Znajdź wzór i dziedzinę funkcji
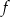 , która zmiennej rzeczywistej
, która zmiennej rzeczywistej 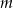 przyporządkowuje iloczyn dwóch różnych pierwiastków danego równania. Naszkicuj wykres funkcji
przyporządkowuje iloczyn dwóch różnych pierwiastków danego równania. Naszkicuj wykres funkcji 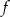 w prostokątnym układzie współrzędnych.
w prostokątnym układzie współrzędnych. - Wykaż, że do wykresu funkcji
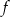 należą tylko trzy punkty o obu współrzędnych całkowitych.
należą tylko trzy punkty o obu współrzędnych całkowitych.
Rozwiązanie
- Sprawdźmy kiedy dane równanie ma dwa różne pierwiastki. Oczywiście musi być kwadratowe, czyli
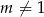 oraz
oraz 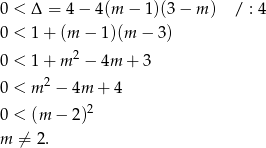
Jeżeli
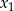 i
i 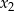 są pierwiastkami danego równania, to na mocy wzorów Vièta’a mamy
są pierwiastkami danego równania, to na mocy wzorów Vièta’a mamy 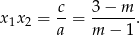
Stąd
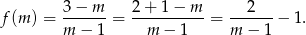
Wykresem tej funkcji jest więc hiperbola
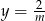 przesunięta o wektor
przesunięta o wektor ![[1,− 1]](https://img.zadania.info/zad/9272500/HzadR7x.gif) , z której usunięto wartość dla
, z której usunięto wartość dla 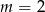 . Bez trudu wykonujemy szkic wykresu.
. Bez trudu wykonujemy szkic wykresu. 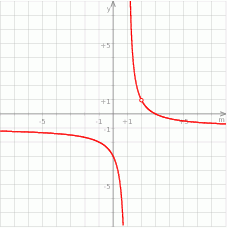
Odpowiedź: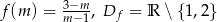
- Jeżeli punkt na wykresie
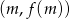 ma obie współrzędne całkowite, to
ma obie współrzędne całkowite, to 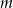 jest całkowite oraz całkowite jest wyrażenie
jest całkowite oraz całkowite jest wyrażenie 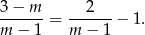
To jednak oznacza, że
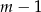 musi dzielić 2. Zatem
musi dzielić 2. Zatem 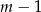 jest jedną z liczb
jest jedną z liczb 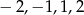 . To daje kolejno
. To daje kolejno 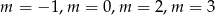 . Ponieważ
. Ponieważ 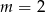 nie należy do dziedziny, daje to trzy punkty wykresu:
nie należy do dziedziny, daje to trzy punkty wykresu: 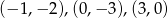 .
.

