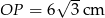Zadanie nr 9328332
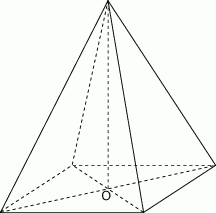
Podstawą ostrosłupa jest romb. Wysokość ostrosłupa ma długość 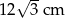 , a spodek
, a spodek  tej wysokości jest punktem przecięcia przekątnych. Każda ze ścian bocznych ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze
tej wysokości jest punktem przecięcia przekątnych. Każda ze ścian bocznych ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze 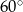 .
.
- Zaznacz na rysunku kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa oraz poprowadź odcinek
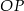 , którego długość jest równa odległości punktu
, którego długość jest równa odległości punktu 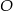 od ściany bocznej.
od ściany bocznej. - Oblicz odległość punktu
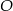 od ściany bocznej.
od ściany bocznej.
Rozwiązanie
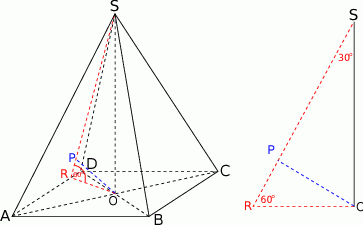
- Rysujemy. Aby zaznaczyć kąt nachylenia ściany
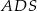 do płaszczyzny podstawy rysujemy odcinek
do płaszczyzny podstawy rysujemy odcinek 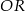 w podstawie prostopadły do krawędzi
w podstawie prostopadły do krawędzi 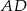 . Kąt nachylenia jest wtedy kątem przy wierzchołku
. Kąt nachylenia jest wtedy kątem przy wierzchołku 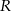 w trójkącie prostokątnym
w trójkącie prostokątnym 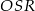 (bo płaszczyzna
(bo płaszczyzna 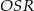 jest jednocześnie prostopadła do płaszczyzny podstawy oraz do ściany bocznej
jest jednocześnie prostopadła do płaszczyzny podstawy oraz do ściany bocznej 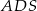 ). Żądany odcinek
). Żądany odcinek 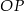 jest wysokością opuszczoną z wierzchołka
jest wysokością opuszczoną z wierzchołka 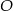 w trójkącie
w trójkącie 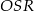 .
. 
- Jeżeli narysujemy z boku trójkąt prostokątny
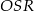 to widać, że długość odcinka
to widać, że długość odcinka 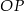 możemy łatwo wyliczyć z trójkąta prostokątnego
możemy łatwo wyliczyć z trójkąta prostokątnego 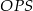 .
. 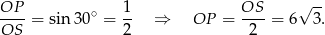
Odpowiedź: