/Szkoła średnia/Zadania maturalne/Matura 2010/Materiały pomocnicze
Zbiór zadań maturalnych
z Matematyki Matura 2010
poziom podstawowy Informator CKE Część 1: zadania zamknięte
Liczba 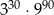 jest równa
jest równa
A) 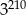 B)
B) 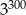 C)
C) 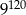 D)
D) 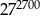
Liczba 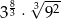 jest równa
jest równa
A) 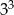 B)
B) 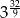 C)
C) 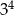 D)
D) 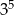
Liczba 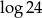 jest równa
jest równa
A) 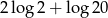 B)
B) 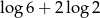 C)
C) 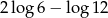 D)
D) 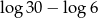
Liczba 30 to 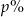 liczby 80, zatem
liczby 80, zatem
A) 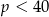 B)
B) 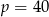 C)
C) 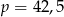 D)
D) 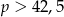
4% liczby  jest równe 6, zatem
jest równe 6, zatem
A) 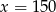 B)
B) 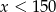 C)
C) 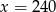 D)
D) 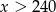
Liczba 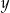 to 120% liczby
to 120% liczby  . Wynika stąd, że
. Wynika stąd, że
A) 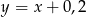 B)
B) 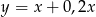 C)
C) 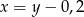 D)
D) 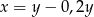
Rozwiązaniem równania 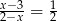 jest liczba
jest liczba
A) 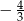 B)
B) 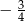 C)
C)  D)
D) 
Mniejszą z dwóch liczb spełniających równanie 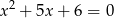 jest
jest
A) -6 B) -3 C) -2 D) -1
Liczba 1 jest miejscem zerowym funkcji liniowej 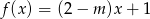 . Wynika stąd, że
. Wynika stąd, że
A) 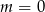 B)
B) 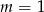 C)
C) 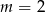 D)
D) 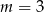
Funkcja 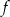 określona jest wzorem
określona jest wzorem
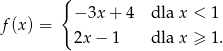
Ile miejsc zerowych ma ta funkcja?
A) 0 B) 1 C) 2 D) 3
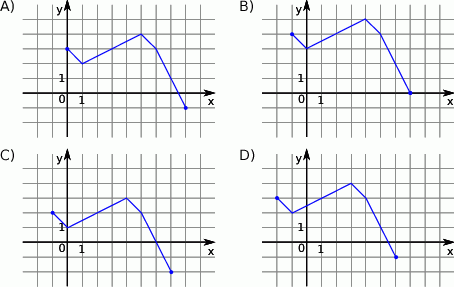
Rysunek przedstawia wykres funkcji 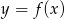 .
.
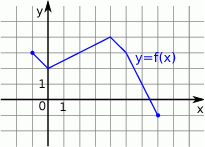
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 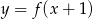 .
.
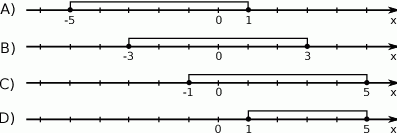
Który z zaznaczonych przedziałów jest zbiorem rozwiązań nierówności 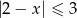 .
.
Wskaż równanie osi symetrii paraboli określonej równaniem 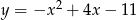 .
.
A) 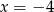 B)
B) 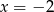 C)
C) 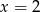 D)
D) 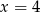
Wskaż funkcję kwadratową, której zbiorem wartości jest przedział 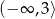 .
.
A) 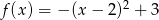
B) 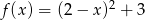
C) 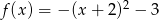
D) 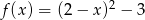
Zbiorem rozwiązań nierówności 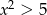 jest
jest
A) 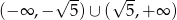 B)
B) 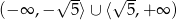 C)
C) 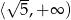 D)
D) 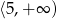
Wykres funkcji kwadratowej 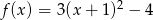 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 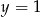 B)
B) 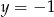 C)
C) 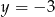 D)
D) 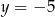
Prosta o równaniu 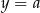 ma dokładnie jeden punkt wspólny z wykresem funkcji kwadratowej
ma dokładnie jeden punkt wspólny z wykresem funkcji kwadratowej 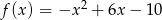 . Wynika stąd, że
. Wynika stąd, że
A) 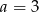 B)
B) 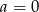 C)
C) 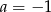 D)
D) 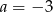
Jaka jest najmniejsza wartość funkcji kwadratowej 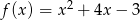 w przedziale
w przedziale 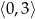 ?
?
A) -7 B) -4 C) -3 D) -2
Dane są wielomiany 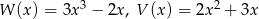 . Stopień wielomianu
. Stopień wielomianu 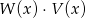 jest równy
jest równy
A) 6 B) 5 C) 4 D) 3
Ile rozwiązań rzeczywistych ma równanie 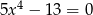 ?
?
A) 1 B) 2 C) 3 D) 4
Wskaż liczbę rozwiązań równania 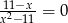 .
.
A) 0 B) 1 C) 2 D) 3
Wskaż równanie prostej równoległej do prostej o równaniu 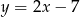 .
.
A) 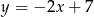 B)
B) 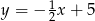 C)
C) 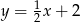 D)
D) 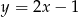
Które z równań opisuje prostą prostopadłą do prostej o równaniu 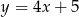 ?
?
A) 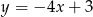 B)
B) 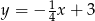 C)
C) 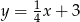 D)
D) 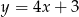
Punkty 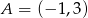 i
i 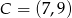 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 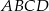 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 10 B) 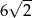 C) 5 D)
C) 5 D) 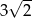
Liczba punktów wspólnych okręgu o równaniu 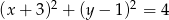 z osiami układu współrzędnych jest równa
z osiami układu współrzędnych jest równa
A) 0 B) 1 C) 2 D) 4
Środek okręgu o równaniu 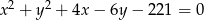 ma współrzędne
ma współrzędne
A) 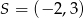 B)
B) 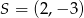 C)
C) 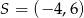 D)
D) 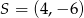
Dane są długości boków 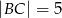 i
i 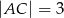 trójkąta prostokątnego
trójkąta prostokątnego 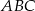 o kącie ostrym
o kącie ostrym 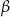 (zobacz rysunek).
(zobacz rysunek).
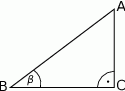
Wtedy
A) 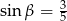 B)
B) 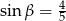 C)
C) 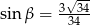 D)
D) 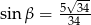
Kąt  jest ostry i
jest ostry i 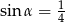 . Wówczas
. Wówczas
A) 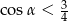 B)
B) 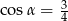 C)
C) 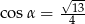 D)
D) 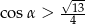
Kąt  jest kątem ostrym i
jest kątem ostrym i 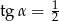 . Jaki warunek spełnia kąt
. Jaki warunek spełnia kąt  ?
?
A) 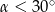 B)
B) 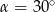 C)
C) 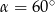 D)
D) 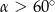
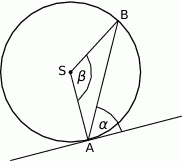
Kąt między cięciwą 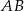 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 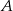 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 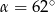 . Wówczas
. Wówczas
A) 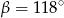 B)
B) 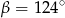 C)
C) 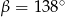 D)
D) 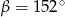
Kąt środkowy i kąt wpisany są oparte na tym samym łuku. Suma ich miar jest równa 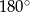 . Jaka jest miara kąta środkowego?
. Jaka jest miara kąta środkowego?
A) 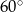 B)
B) 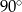 C)
C) 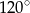 D)
D) 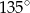
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 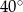 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 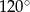 B)
B) 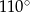 C)
C) 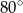 D)
D) 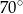
Odcinki 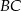 i
i 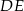 są równoległe. Długości odcinków
są równoległe. Długości odcinków 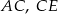 i
i 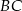 są podane na rysunku.
są podane na rysunku.
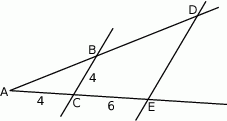
Długość odcinka 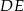 jest równa
jest równa
A) 6 B) 8 C) 10 D) 12
Pole kwadratu wpisanego w okrąg o promieniu 4 cm jest równe
A) 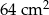 B)
B) 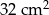 C)
C) 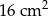 D)
D) 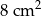
Ciąg 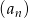 jest określony wzorem
jest określony wzorem 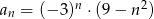 dla
dla 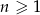 . Wynika stąd, że
. Wynika stąd, że
A) 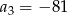 B)
B) 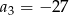 C)
C) 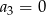 D)
D) 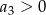
Liczby 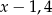 i 8 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Wówczas liczba
i 8 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Wówczas liczba  jest równa
jest równa
A) 3 B) 1 C) -1 D) -7
Liczby -8,4 i 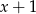 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba
(w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba  jest równa
jest równa
A) -3 B) -1,5 C) 1 D) 15
Wszystkich liczb naturalnych dwucyfrowych, które są podzielne przez 6 lub przez 10, jest
A) 25 B) 24 C) 21 D) 20
Wszystkich liczb naturalnych dwucyfrowych, których obie cyfry są mniejsze od 5 jest
A) 16 B) 20 C) 25 D) 30
Liczba sposobów, na jakie Ala i Bartek mogą usiąść na dwóch spośród pięciu miejsc w kinie, jest równa
A) 25 B) 20 C) 15 D) 12
Mediana danych: 0, 1, 1, 2, 3, 1 jest równa
A) 1 B) 1,5 C) 2 D) 2,5
Mediana danych przedstawionych w tabeli liczebności jest równa
| Wartość | 0 | 1 | 2 | 3 |
| Liczebność | 5 | 2 | 1 | 1 |
A) 0 B) 0,5 C) 1 D) 5
Średnia arytmetyczna danych przedstawionych na diagramie częstości jest równa
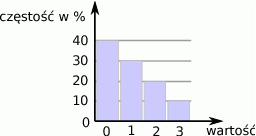
A) 1 B) 1,2 C) 1,5 D) 1,8
Ze zbioru liczb 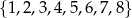 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 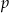 oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy
oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy
A) 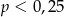 B)
B) 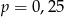 C)
C) 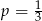 D)
D) 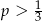
O zdarzeniach losowych 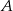 i
i 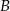 zawartych w
zawartych w 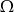 wiadomo, że
wiadomo, że 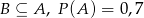 i
i 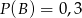 . Wtedy
. Wtedy
A) 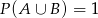 B)
B) 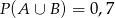 C)
C) 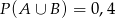 D)
D) 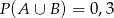
Przekątna sześcianu ma długość 3. Pole powierzchni całkowitej tego sześcianu jest równe
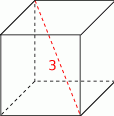
A) 54 B) 36 C) 18 D) 12
Pole powierzchni całkowitej sześcianu jest równe 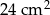 . Objętość tego sześcianu jest równa
. Objętość tego sześcianu jest równa
A) 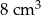 B)
B) 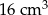 C)
C) 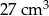 D)
D) 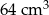
Przekątna prostopadłościanu o wymiarach 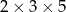 ma długość
ma długość
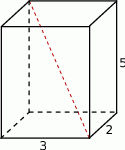
A) 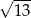 B)
B) 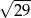 C)
C) 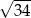 D)
D) 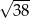
Przekrój osiowy walca jest kwadratem o boku długości 6. Objętość tego walca jest równa
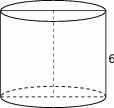
A) 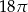 B)
B) 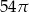 C)
C) 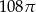 D)
D) 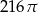
Przekrój osiowy stożka jest trójkątem równobocznym o boku długości 6.
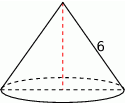
Pole powierzchni bocznej tego stożka jest równe
A) 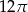 B)
B) 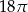 C)
C) 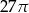 D)
D)