/Szkoła średnia/Funkcje/Trygonometryczna/Tożsamości

Zadanie nr 5481001

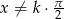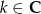Wykaż, że jeżeli π- x ⁄= k⋅ 2 dla k ∈ C to prawdziwa jest tożsamość

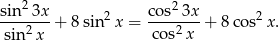
2 2 sin-3x-+ 8sin2 x = cos--3x + 8 cos2x . sin 2x cos2x
Wersja PDF

Rozwiązanie

Sposób I

Przekształcamy tożsamość korzystając ze wzoru na 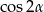cos 2α i wzoru skróconego mnożenia na różnicę kwadratów.

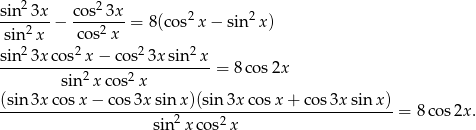
2 2 sin--3x-− cos-3x-= 8(cos2 x− sin 2x) sin2x cos2 x sin 23x cos2x − co s2 3x sin 2x -----------------------------= 8cos 2x sin2x cos2x (sin-3x-cosx-−-co-s3x-sin-x)(sin-3xco-sx-+-cos-3x-sin-x)- 2 2 = 8 cos 2x. sin xco s x

Teraz korzystamy ze wzorów na sinus sumy i różnicy.

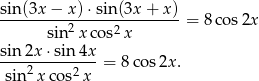
sin(3x-−--x)⋅sin(3x-+--x) = 8 cos2x sin 2x cos2x sin-2x-⋅sin-4x- 2 2 = 8co s2x. sin x cos x

Teraz korzystamy ze wzoru na 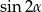sin 2α .

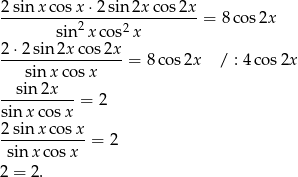
2sin xco sx ⋅2sin 2xco s2x ----------2-----2----------= 8co s2x sin xcos x 2⋅-2sin2x-cos-2x-= 8cos 2x / : 4co s2x sinx cos x sin2x ---------- = 2 sin x cosx 2sin-xco-sx-= 2 sin x cosx 2 = 2.

Sposób II

Przekształcamy tożsamość korzystając ze wzoru na 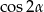cos 2α i wzoru skróconego mnożenia na różnicę kwadratów.

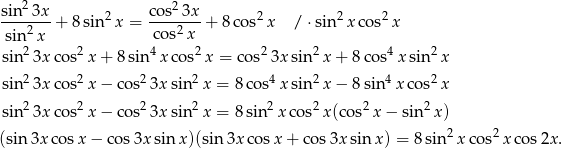
sin23x- 2 co-s23x 2 2 2 2 + 8sin x = cos2x + 8 cos x / ⋅sin x cos x sin2 x 2 4 2 2 2 4 2 sin 3xco s x + 8sin xco s x = co s 3x sin x + 8 cos x sin x sin2 3xco s2x − cos23x sin2 x = 8 cos4x sin 2x − 8 sin 4x cos2x sin2 3xco s2x − cos23x sin2 x = 8 sin2 xco s2x(co s2x − sin2x) 2 2 (sin 3x cos x− cos3x sinx )(sin 3x cosx + co s3x sin x) = 8sin x cos xcos 2x.

Teraz korzystamy ze wzorów na sinus sumy i różnicy oraz ze wzoru na 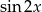sin 2x .

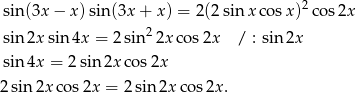
2 sin(3x − x) sin (3x + x) = 2 (2sinx cos x) cos 2x sin2x sin 4x = 2 sin 22x cos2x / : sin 2x sin4x = 2 sin 2x cos2x 2sin 2xco s2x = 2sin2x cos 2x.

Sposób III

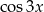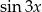Tym razem wyprowadzimy najpierw wzory na cos3x i sin3x . Liczymy

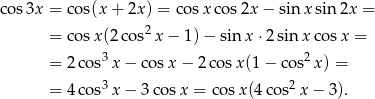
co s3x = co s(x+ 2x) = co sx cos2x − sin xsin 2x = = co sx(2 cos2x − 1 )− sin x⋅ 2sinx cos x = = 2 cos3 x− cosx − 2 cosx (1− cos2x) = 3 2 = 4 cos x− 3cos x = cos x(4 cos x − 3).

Podobnie liczymy 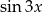sin3x .

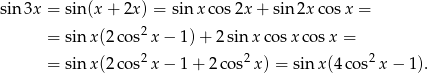
sin 3x = sin (x+ 2x) = sin xcos 2x + sin2x cos x = = sin x(2 cos2x − 1) + 2 sin x cosx cos x = 2 2 2 = sin x(2 cos x − 1 + 2 cos x ) = sin x(4 cos x − 1).

Teraz bez trudu wyprowadzamy tożsamość z treści zadania.

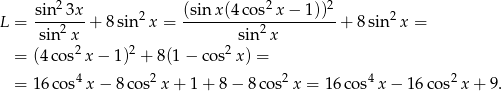
sin2 3x (sin x(4 cos2x − 1))2 L = ------- + 8 sin 2x = ---------------------+ 8 sin2x = sin2x sin2 x = (4 cos2x − 1)2 + 8(1 − co s2 x) = 4 2 2 4 2 = 16 cos x − 8 cos x+ 1+ 8− 8 cos x = 16 cos x − 16 cos x+ 9.

Z drugiej strony,

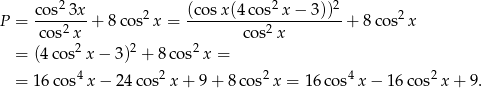
cos23x (cosx(4 cos2 x− 3))2 P = ----2-- + 8co s2x = ----------2----------+ 8cos2 x co s x cos x = (4cos2 x− 3)2 + 8cos2 x = 4 2 2 4 2 = 16co s x − 24 cos x + 9 + 8 cos x = 16co s x − 16 cos x + 9.

Zatem rzeczywiście 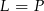L = P .

Wersja PDF