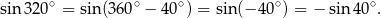Zadanie nr 6811428
Wykaż, że 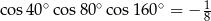 .
.
Rozwiązanie
Będziemy kilkukrotnie korzystać ze wzoru
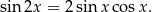
Przekształcamy równość, którą mamy udowodnić w sposób równoważny.
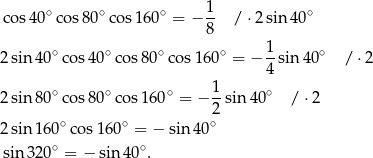
Teraz wystarczy zauważyć, że faktycznie
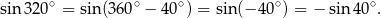
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że 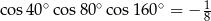 .
.
Będziemy kilkukrotnie korzystać ze wzoru
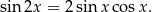
Przekształcamy równość, którą mamy udowodnić w sposób równoważny.
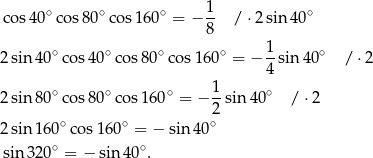
Teraz wystarczy zauważyć, że faktycznie