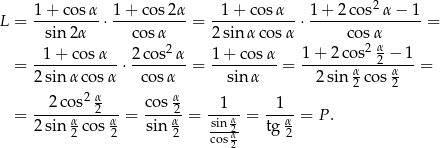Zadanie nr 7357960
Wykaż, że jeżeli 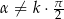 , gdzie
, gdzie 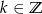 , to
, to
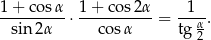
Rozwiązanie
Korzystamy ze wzorów
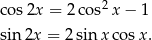
Przekształcamy lewą stronę tożsamości (zamieniamy konsekwentnie kąty tak, aby wszędzie mieć 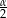 ).
).
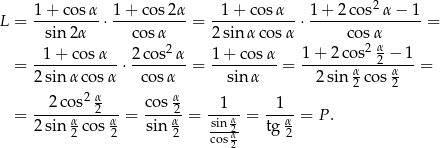
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że jeżeli 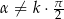 , gdzie
, gdzie 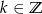 , to
, to
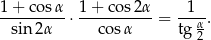
Korzystamy ze wzorów
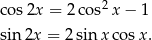
Przekształcamy lewą stronę tożsamości (zamieniamy konsekwentnie kąty tak, aby wszędzie mieć 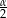 ).
).