/Studia/Analiza/Ciągi/Monotoniczność

Zadanie nr 7433443

Dodaj do ulubionych
Dodaj do rozwiązanych

Zbadaj monotoniczność ciągu określonego wzorem 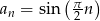(π- ) an = sin 2n .

Rozwiązanie

Licząc kilka początkowych wyrazów ciągu łatwo zauważyć, że wyrazy o numerach parzystych są równe 0, a wyrazy o numerach nieparzystych są na zmianę równe 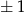± 1 . Tak jest, bo

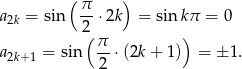
( ) a2k = sin π- ⋅2k = sin kπ = 0 2( ) a = sin π-⋅(2k + 1) = ± 1. 2k+ 1 2

Zatem ciąg nie jest monotoniczny.  
Odpowiedź: Nie jest monotoniczny.

Wersja PDF