Zadanie nr 9346873
Z talii 52 kart losujemy dwa razy po jednej karcie (ze zwracaniem). Niech 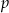 oznacza prawdopodobieństwo wylosowania dwóch królów. Wtedy
oznacza prawdopodobieństwo wylosowania dwóch królów. Wtedy
A) 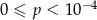 B)
B) 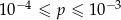 C)
C) 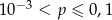 D)
D) 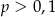
Rozwiązanie
Jeżeli o wynikach myślimy jak o parach wylosowanych kart, to
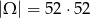
(w pierwszym losowaniu mamy 52 możliwości i w drugim też).
Wszystkie zdarzenie sprzyjające są postaci 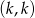 , gdzie na obu miejscach mamy króla. W talii są jednak 4 króle, więc wszystkich zdarzeń sprzyjających jest
, gdzie na obu miejscach mamy króla. W talii są jednak 4 króle, więc wszystkich zdarzeń sprzyjających jest
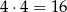
(każdego z króli możemy wybrać na 4 sposoby). Mamy zatem
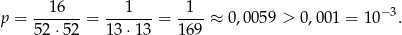
Odpowiedź: C

