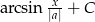Zadanie nr 7787072
Oblicz całkę 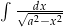 .
.
Rozwiązanie
Podstawiamy 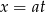 .
.
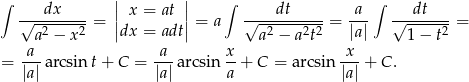
Ostatnie przejście było możliwe dzięki temu, że 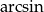 jest funkcją nieparzystą. Jeżeli ktoś ma wątpliwości, to niech rozważy dwa przypadki:
jest funkcją nieparzystą. Jeżeli ktoś ma wątpliwości, to niech rozważy dwa przypadki: 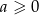 i
i 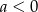 .
.
Odpowiedź: 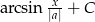
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 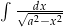 .
.
Podstawiamy 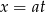 .
.
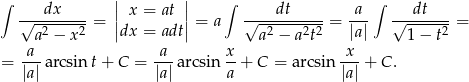
Ostatnie przejście było możliwe dzięki temu, że 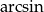 jest funkcją nieparzystą. Jeżeli ktoś ma wątpliwości, to niech rozważy dwa przypadki:
jest funkcją nieparzystą. Jeżeli ktoś ma wątpliwości, to niech rozważy dwa przypadki: 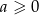 i
i 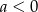 .
.
Odpowiedź: