Zadanie nr 3845972
Wskaż równanie prostej równoległej do prostej o równaniu 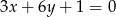 .
.
A) 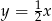 B)
B) 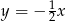 C)
C) 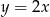 D)
D) 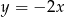
Rozwiązanie
Proste 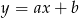 i
i 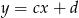 są równoległe jeżeli mają takie same współczynniki kierunkowe, czyli gdy
są równoległe jeżeli mają takie same współczynniki kierunkowe, czyli gdy  .
.
Dane równanie prostej możemy zapisać w postaci
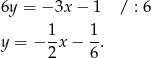
Jej współczynnik kierunkowy jest więc równy 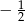 , czyli prostą do niej równoległą jest prosta
, czyli prostą do niej równoległą jest prosta 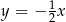 .
.
Odpowiedź: B

