Zadanie nr 9278081
Na której z podanych prostych leżą wszystkie punkty o współrzędnych 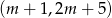 , gdzie
, gdzie 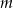 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 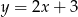 B)
B) 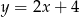 C)
C) 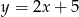 D)
D) 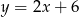
Rozwiązanie
Sposób I
Zauważmy, że jeżeli 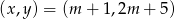 , to
, to
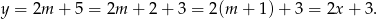
To oznacza, że punkty o danych współrzędnych leżą na prostej 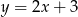 .
.
Sposób II
W każdej z podanych prostych współczynnik kierunkowy jest równy 2, więc obliczamy 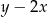 dla
dla 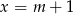 i
i 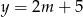 .
.
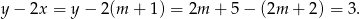
Zatem 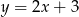 .
.
Sposób III
Dla 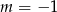 otrzymujemy punkt
otrzymujemy punkt 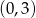 . Wśród podanych odpowiedzi tylko prosta
. Wśród podanych odpowiedzi tylko prosta 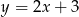 przechodzi przez ten punkt.
przechodzi przez ten punkt.
Odpowiedź: A

