/Szkoła średnia/Zadania testowe/Prawdopodobieństwo/Różne

Zadanie nr 6946955

Kod dostępu do sejfu składa się z pięciu cyfr. Chcemy, aby prawdopodobieństwo odkrycia tego kodu zmniejszyło się stukrotnie. Ile cyfr powinien mieć nowy kod?
A) 7 B) 2 C) 100 D) 6

Wersja PDF

Rozwiązanie

Jeżeli kod składa się z n cyfr od 0 do 9, to wszystkich możliwych kodów jest

|Ω | = 10n

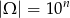
(każdą cyfrę możemy wybrać na 10 sposobów). Zatem jeżeli kod jest pięciocyfrowy to prawdopodobieństwo zgadnięcia kodu jest równe

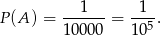
--1--- -1-- P(A ) = 10000 = 105.

Wyznaczamy n tak, aby prawdopodobieństwo zmniejszyły się do -1- 107 .

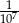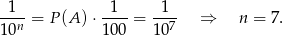
-1-- -1-- -1-- 10n = P (A )⋅ 100 = 107 ⇒ n = 7.

Kod musi się więc składać z 7 cyfr.  
Odpowiedź: A

Wersja PDF