/Studia/Analiza/Całki nieoznaczone/Wymierne/Mianownik stopnia 2

Zadanie nr 2759642

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz całkę 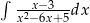∫ --x−3--- x2− 6x+5dx .

Rozwiązanie

Funkcja podcałkowa jest sumą dwóch ułamków prostych pierwszego rodzaju, bo mianownik ma dwa pierwiastki rzeczywiste (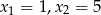x1 = 1,x2 = 5 ). Jednak zamiast rozkładać tą funkcję na ułamki proste, lepiej jest zauważyć, że licznik jest równy pochodnej mianownika podzielonej przez 2. Zatem najprościej jest całkować przez podstawienie.

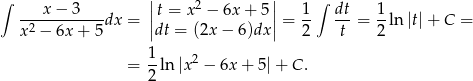
| | ∫ x − 3 |t = x2 − 6x + 5 | 1 ∫ dt 1 --2---------dx = || || = -- ---= --ln |t|+ C = x − 6x + 5 dt = (2x − 6)dx 2 t 2 1- 2 = 2 ln |x − 6x+ 5|+ C .

 
Odpowiedź: 1 2 2 ln|x − 6x + 5| + C

Wersja PDF