/Studia/Analiza/Całki nieoznaczone/Wymierne/Mianownik stopnia 2

Zadanie nr 4304109

Oblicz całkę 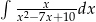∫ ---x----- x2− 7x+10dx .

Wersja PDF

Rozwiązanie

Rozkładamy mianownik na czynniki.

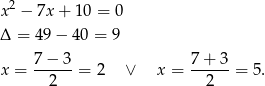
2 x − 7x + 10 = 0 Δ = 49− 40 = 9 7 − 3 7+ 3 x = ------= 2 ∨ x = ------= 5 . 2 2

Szukamy zatem rozkładu funkcji podcałkowej na ułamki proste postaci

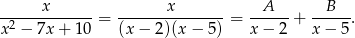
x x A B -2-----------= ---------------= ------+ ------. x − 7x + 10 (x − 2)(x − 5) x − 2 x − 5

Mnożąc obie strony przez 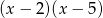(x− 2)(x− 5) otrzymujemy

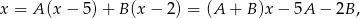
x = A (x− 5)+ B(x − 2) = (A + B )x− 5A − 2B ,

co daje układ równań

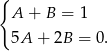
{ A + B = 1 5A + 2B = 0.

Odejmując od drugiego równania pierwsze pomnożone przez 2 (żeby zredukować 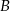B ) otrzymujemy 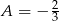2 A = − 3 . Stąd 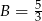5 B = 3 oraz

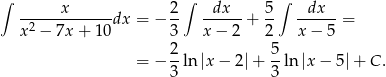
∫ ∫ ∫ ------x------dx = − 2- --dx--+ 5- --dx--= x 2 − 7x + 10 3 x − 2 2 x − 5 2- 5- = − 3 ln |x− 2|+ 3 ln |x − 5|+ C .

 
Odpowiedź: − 2 ln |x− 2|+ 5ln|x − 5| + C 3 3

Wersja PDF