/Studia/Analiza/Całki nieoznaczone/Wymierne/Mianownik stopnia 2

Zadanie nr 8585680

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz całkę 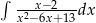∫ --x−-2--- x2− 6x+13dx .

Rozwiązanie

Całkę rozbijamy na dwie całki tak, aby w jednej licznik był pochodną mianownika, a w drugiej, żeby nie było x w liczniku.

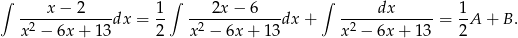
∫ ∫ ∫ ----x-−-2----dx = 1- ---2x-−--6---dx + -----dx------= 1-A + B . x 2 − 6x + 13 2 x 2 − 6x + 13 x2 − 6x + 13 2

Liczymy teraz te prostsze całki 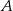A i B .

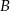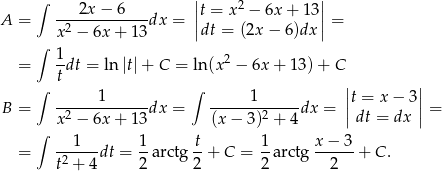
∫ | | ----2x−--6--- ||t = x2 − 6x + 13 || A = x 2 − 6x + 13dx = |dt = (2x − 6)dx | = ∫ = 1-dt = ln|t|+ C = ln(x2 − 6x + 1 3)+ C t | | ∫ 1 ∫ 1 |t = x− 3| B = --2----------dx = -------2----dx = || || = ∫ x − 6x + 13 (x− 3) + 4 dt = dx ---1-- 1- t- 1- x−--3- = t2 + 4dt = 2 arctg 2 + C = 2 arctg 2 + C .

Przy liczeniu drugiej całki skorzystaliśmy ze wzoru

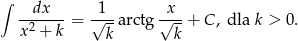
∫ --dx---= √1--arctg √x--+ C, dla k > 0. x 2 + k k k

Mamy zatem

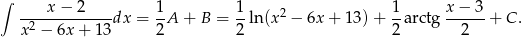
∫ x− 2 1 1 1 x − 3 -------------dx = -A + B = -ln(x 2 − 6x + 13)+ --arctg ------+ C . x2 − 6x + 13 2 2 2 2

 
Odpowiedź: 1 ln (x2 − 6x + 13) + 1 arctg x−-3+ C 2 2 2

Wersja PDF