Zadanie nr 4902962
Oblicz całkę 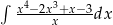 .
.
Rozwiązanie
Liczenie całki nieoznaczonej 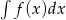 to szukanie funkcji
to szukanie funkcji 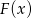 takiej, że
takiej, że 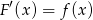 . Podany przykład jest na tyle prosty, że możemy funkcję
. Podany przykład jest na tyle prosty, że możemy funkcję 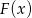 zgadnąć z odpowiednich wzorów na pochodne. Liczymy
zgadnąć z odpowiednich wzorów na pochodne. Liczymy
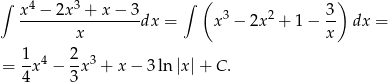
Odpowiedź: 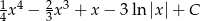
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 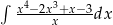 .
.
Liczenie całki nieoznaczonej 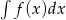 to szukanie funkcji
to szukanie funkcji 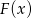 takiej, że
takiej, że 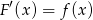 . Podany przykład jest na tyle prosty, że możemy funkcję
. Podany przykład jest na tyle prosty, że możemy funkcję 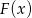 zgadnąć z odpowiednich wzorów na pochodne. Liczymy
zgadnąć z odpowiednich wzorów na pochodne. Liczymy
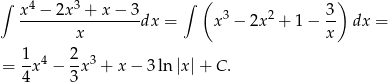
Odpowiedź: