/Studia/Analiza/Całki nieoznaczone/Wymierne/Mianownik stopnia 3

Zadanie nr 4463989

Oblicz całkę 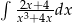∫ 2x+4- x3+ 4xdx .

Wersja PDF

Rozwiązanie

Ponieważ

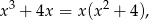
3 2 x + 4x = x (x + 4),

szukamy rozkładu funkcji podcałkowej na ułamki proste postaci

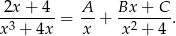
2x+ 4 A Bx + C --------= -- + --------. x3 + 4x x x2 + 4

Mnożąc obie strony przez 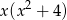2 x(x + 4) otrzymujemy

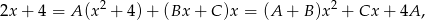
2 2 2x + 4 = A (x + 4) + (Bx + C)x = (A + B )x + Cx + 4A ,

co daje układ równań

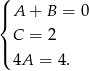
( |{ A + B = 0 C = 2 |( 4A = 4.

Zatem 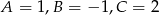A = 1,B = − 1,C = 2 oraz

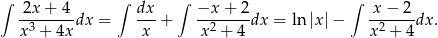
∫ 2x + 4 ∫ dx ∫ −x + 2 ∫ x − 2 -3-----dx = ---+ --2----dx = ln|x|− -2----dx. x + 4x x x + 4 x + 4

Zajmiemy się teraz ostatnią całką – będziemy korzystać ze wzoru

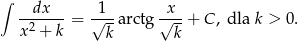
∫ --dx--- -1-- -x-- x 2 + k = √k--arctg √k--+ C, dla k > 0.

Liczymy

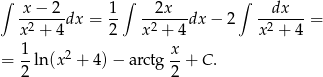
∫ ∫ ∫ x-−-2-- 1- --2x--- --dx--- x2 + 4dx = 2 x 2 + 4 dx − 2 x 2 + 4 = = 1-ln (x2 + 4)− arctg x-+ C. 2 2

Zatem

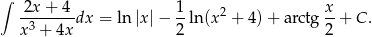
∫ 2x + 4 1 x --3-----dx = ln |x|− -ln(x 2 + 4 )+ arctg--+ C . x + 4x 2 2

 
Odpowiedź: 1 2 x ln |x|− 2 ln(x + 4) + arctg 2 + C

Wersja PDF