Zadanie nr 3185238
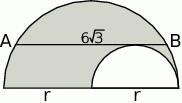
Z półkola o promieniu  wycięto półkole o średnicy
wycięto półkole o średnicy  (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa 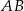 jest styczna do mniejszego półkola i jest równoległa do średnicy większego półkola. Oblicz pole zacieniowanego obszaru.
jest styczna do mniejszego półkola i jest równoległa do średnicy większego półkola. Oblicz pole zacieniowanego obszaru.
Rozwiązanie
Niech 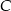 będzie środkiem cięciwy
będzie środkiem cięciwy 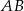 , a
, a 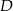 środkiem większego półkola.
środkiem większego półkola.
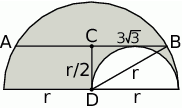
W trójkącie prostokątnym 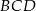 odcinek
odcinek 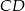 ma długość równą promieniowi mniejszego półkola, a odcinek
ma długość równą promieniowi mniejszego półkola, a odcinek 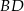 długość równą promieniowi większego półkola. W takim razie na mocy twierdzenia Pitagorasa mamy
długość równą promieniowi większego półkola. W takim razie na mocy twierdzenia Pitagorasa mamy
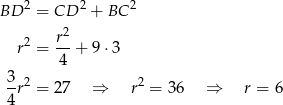
Pole zacieniowanego obszaru jest więc równe
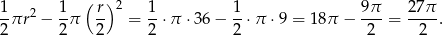
Odpowiedź: