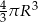/Studia/Analiza/Zastosowania całek/Objętość

Zadanie nr 6643351

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz objętość kuli o promieniu 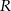R .

Rozwiązanie

Sposób I

Korzystamy ze wzoru

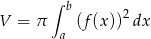
∫ b 2 V = π a (f(x )) dx

na objętość bryły otrzymanej przez obrót wokół osi 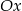Ox obszaru zawartego pod wykresem funkcji 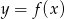y = f(x) , gdzie x ∈ [a,b] .

PIC

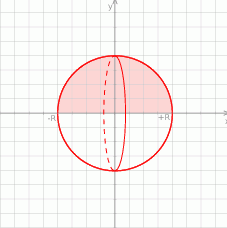
Kula o promieniu 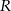R powstaje z obrotu wokół osi 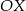OX półkola 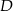D opisanego nierównościami

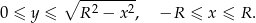
∘ --2----2 0 ≤ y ≤ R − x , −R ≤ x ≤ R .

Zatem jej objętość równa się

∫ R ( ∘ --------)2 ∫ R π R 2 − x 2 dx = π (R 2 − x 2)dx = −R −R ∫ R [ 1 ]R 4πR 3 = 2π (R2 − x2)dx = 2π R 2x − --x3 = -----. 0 3 0 3

Sposób II

Jeżeli nie chcemy korzystać z gotowego wzoru na objętość bryły obrotowej, możemy policzyć całkę potrójną

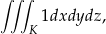
∫∫∫ 1dxdydz , K

gdzie 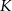K jest kulą o promieniu 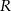R . Aby obliczyć tę całkę zmieniamy współrzędne na sferyczne.

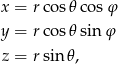
x = r cos𝜃 cosφ y = r cos𝜃 sin φ z = r sin 𝜃,

gdzie π- π- r ∈ [0,R ], φ ∈ [0,2π ], 𝜃 ∈ [− 2 ,2] .

PIC

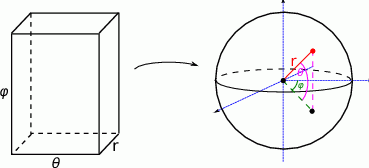
Liczymy jakobian zmiany zmiennych.

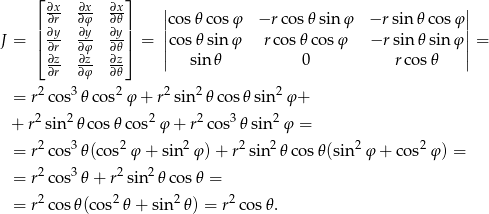
⌊ ∂x ∂x- ∂x ⌋ | | ∂r ∂φ ∂𝜃 |cos𝜃 cosφ −r cos 𝜃sinφ −r sin𝜃 cos φ| J = || ∂y ∂y- ∂y-|| = ||cos𝜃 sin φ r cos𝜃 cos φ −r sin 𝜃sinφ ||= ⌈ ∂∂rz ∂∂φz ∂𝜃∂z ⌉ || || ∂r ∂φ- ∂𝜃- sin 𝜃 0 r cos𝜃 2 3 2 2 2 2 = r cos 𝜃cos φ + r sin 𝜃cos 𝜃sin φ+ + r2 sin 2𝜃co s𝜃 cos2φ + r2 cos3𝜃 sin 2φ = = r2cos3 𝜃(cos2φ + sin 2φ) + r2sin2 𝜃co s𝜃(sin2φ + cos2φ ) = 2 3 2 2 = r cos 𝜃 + r sin 𝜃 cos𝜃 = = r2cos 𝜃(cos2𝜃 + sin2 𝜃) = r2cos 𝜃.

Zatem

∫∫ ∫ ∫ R ∫ π ∫ 2π 1dxdydz = 2 r2co s𝜃dφd 𝜃dr = K 0 − π2 0 ∫ R ∫ π (∫ 2π ) ∫ R ( ∫ π ) = 2 r2 cos𝜃 1dφ d𝜃dr = 2π r2 2 co s𝜃d𝜃 dr = 0 − π2 0 0 − π2 ∫ R ( π ) ∫ R [ ]R = 2π r2 [sin 𝜃]2π dr = 4π r2dr = 4π 1r3 = 4πR 3. 0 −2 0 3 0 3

Sposób III

Skorzystamy z trójwymiarowej wersji twierdzenia Stokesa, czyli z twierdzenia
Gaussa-Ostrogradskiego

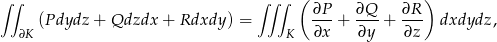
( ) ∫∫ ∫ ∫∫ ∂P ∂Q ∂R (P dydz + Qdzdx + Rdxdy ) = ---+ ---+ --- dxdydz , ∂K K ∂x ∂y ∂z

gdzie 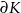∂K jest dodatnio zorientowaną powierzchnią bryły K .

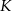Chcemy, aby z prawej strony powyższego wzoru była całka 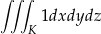∫ ∫∫ K 1dxdydz , więc podstawmy 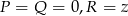P = Q = 0,R = z . Mamy zatem

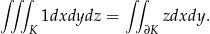
∫∫∫ ∫∫ 1dxdydz = zdxdy . K ∂K

Aby obliczyć całkę powierzchniową z prawej strony, używamy parametryzacji sferycznej

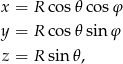
x = R cos 𝜃cos φ y = R cos 𝜃sin φ z = R sin𝜃 ,

gdzie π- π- φ ∈ [0,2π ], 𝜃 ∈ [− 2 ,2] . Mamy wtedy

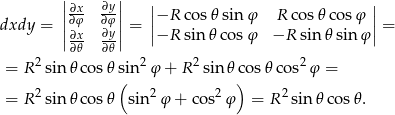
||∂x- ∂y|| || || dxdy = ||∂φ ∂φ||= |−R cos 𝜃sin φ R cos𝜃 cosφ |= |∂x ∂y| |−R sin𝜃 cos φ −R sin𝜃 sin φ | 2 ∂𝜃 ∂𝜃 2 2 2 = R sin𝜃 cos 𝜃sin φ + R sin 𝜃c os𝜃 cos φ = 2 ( 2 2 ) 2 = R sin𝜃 cos 𝜃 sin φ + cos φ = R sin 𝜃 cos𝜃.

Zatem

∫ ∫ ∫ π ∫ 2 2π 2 ∂K zdxdy = − π 0 R sin𝜃 ⋅R sin𝜃 cos 𝜃dφd 𝜃 = ∫ π 2 (∫ ) ∫ π 3 2 2 2π 3 2 2 = R − π sin 𝜃 cos𝜃 0 1d φ d𝜃 = 2πR −π sin 𝜃 cos𝜃d φ = 2[ ]π 2 3 1- 3 2 4- 3 = 2πR 3 sin 𝜃 πd φ = 3 πR . − 2

 
Odpowiedź: 4πR 3 3

Wersja PDF