/Szkoła średnia/Zadania maturalne/Matura 2011/Matura próbna/CKE, OKE, CEN

Próbny Egzamin Maturalny
z Matematyki (OKE Poznań)
poziom rozszerzony 13 stycznia 2011 Czas pracy: 180 minut

Zadanie 1
(4 pkt)

Rozwiąż nierówność 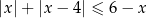|x|+ |x − 4| ≤ 6− x .

Zadanie 2
(4 pkt)

Wielomian 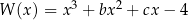W (x) = x3 + bx2 + cx − 4 jest podzielny przez trójmian kwadratowy 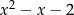x 2 − x − 2 . Wyznacz współczynniki 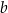b i c wielomianu W (x) .

Zadanie 3
(4 pkt)

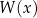Wyznacz wszystkie rozwiązania równania 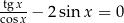tgx-− 2 sin x = 0 cosx .

Zadanie 4
(4 pkt)

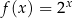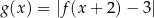Narysuj wykres funkcji f (x) = 2x , a następnie narysuj wykres funkcji g(x ) = |f(x + 2)− 3| .

Zadanie 5
(4 pkt)

Dany jest okrąg o równaniu 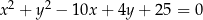x2 + y2 − 10x + 4y + 25 = 0 . Napisz równania stycznych do tego okręgu, przechodzących przez początek układu współrzędnych.

Zadanie 6
(4 pkt)

Wykaż, że w dowolnym równoległoboku suma kwadratów długości przekątnych jest równa sumie kwadratów długości wszystkich boków.

Zadanie 7
(4 pkt)

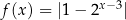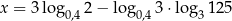Oblicz wartość funkcji x−3 f (x) = |1− 2 | dla argumentu x = 3log0,42 − log0,4 3⋅log 3125 .

Zadanie 8
(5 pkt)

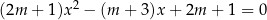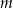Dane jest równanie 2 (2m + 1)x − (m + 3)x + 2m + 1 = 0 z niewiadomą x . Wyznacz te wartości parametru m , dla których suma odwrotności różnych pierwiastków danego równania jest większa od 1.

Zadanie 9
(4 pkt)

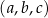Ciąg (a,b,c) jest ciągiem arytmetycznym. Suma jego wyrazów jest równa 18. Jeżeli pierwszą z liczb zmniejszymy o 25%, a trzecią zwiększymy o 50%, to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Wyznacz liczby a,b,c .

Zadanie 10
(4 pkt)

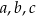Krawędź podstawy ostrosłupa trójkątnego prawidłowego jest równa 6. Jego objętość jest równa 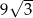√ -- 9 3 . Wyznacz długość wysokości ściany bocznej ostrosłupa.

Zadanie 11
(4 pkt)

Wśród dziesięciu losów loteryjnych znajduje się jeden los z główną wygraną oraz dwa losy uprawniające do wylosowania następnego losu. Oblicz prawdopodobieństwo wygrania przy zakupie jednego losu.

Zadanie 12
(5 pkt)

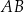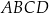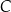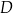Dany jest równoramienny trójkąt prostokątny, którego przeciwprostokątna ma długość 2. Bok AB prostokąta ABCD zawiera się w przeciwprostokątnej tego trójkąta, zaś punkty C i D należą do przyprostokątnych. Oblicz długości boków prostokąta 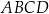ABCD wiedząc, że kwadrat długości jego przekątnej 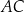AC ma wartość najmniejszą z możliwych.

Arkusz Wersja PDF
Rozwiązania