/Szkoła podstawowa/Geometria/Trójkąt/Prostokątny

Zadanie nr 8755616

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie prostokątnym jedna z przyprostokątnych ma długość 10 cm, a przeciwprostokątna jest o 2 cm dłuższa od drugiej przyprostokątnej. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego.

Rozwiązanie

Szkicujemy trójkąt prostokątny.

PIC

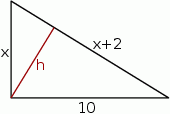
Na mocy twierdzenia Pitagorasa mamy równanie

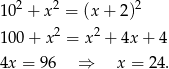
2 2 2 10 + x = (x+ 2) 10 0+ x2 = x2 + 4x + 4 4x = 96 ⇒ x = 24.

Zatem przeciwprostokątna ma długość 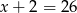x + 2 = 26 i pole trójkąta jest równe

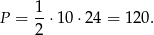
1- P = 2 ⋅10 ⋅24 = 120.

Wysokość 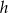h opuszczoną z wierzchołka kąta prostego obliczamy porównując dwa wzory na pole trójkąta.

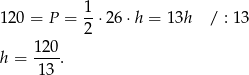
1- 120 = P = 2 ⋅2 6⋅h = 13h / : 13 1 20 h = ----. 13

 
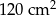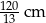Odpowiedź: Pole: 2 120 cm , wysokość: 12103 cm .

Wersja PDF