Zadanie nr 9358620
Uzasadnij, że jeśli 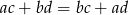 to
to 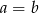 lub
lub 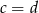 .
.
Rozwiązanie
Sposób I
Jeżeli zapiszemy daną równość w postaci
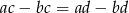
to widać, że po obu stronach można wyłączyć 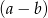 przed nawias.
przed nawias.
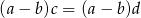
Zatem albo 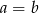 , albo możemy podzielić tę równość stronami przez
, albo możemy podzielić tę równość stronami przez 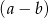 i wtedy
i wtedy 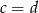 .
.
Sposób II
Przekształćmy daną równość.
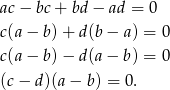
Zatem 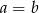 lub
lub 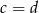 .
.

