Zadanie nr 4694164
Kasia napisała na tablicy 6 kolejnych wielokrotności liczby 9. Uzasadnij, że suma pierwszych trzech z tych liczb jest o 81 mniejsza od sumy trzech ostatnich.
Rozwiązanie
Sposób I
Sześć kolejnych wielokrotności liczby 9 możemy oznaczyć przez
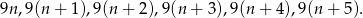
Suma pierwszych trzech z tych liczb to
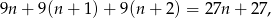
a suma trzech następnych to
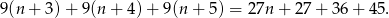
Widać teraz, że druga z tych sum jest większa od pierwszej o 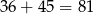 .
.
Sposób II
Sześć kolejnych wielokrotności liczby 9 możemy oznaczyć przez
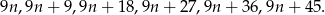
Suma pierwszych trzech z tych liczb to
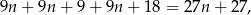
a suma trzech następnych to
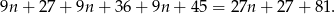
Widać teraz, że druga z tych sum jest większa od pierwszej o 81.

