Średnia arytmetyczna liczb: 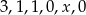 jest równa 2. Oblicz
jest równa 2. Oblicz  .
.
/Szkoła podstawowa/Statystyka
Średnia arytmetyczna liczb 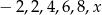 jest równa 5. Wyznacz liczbę
jest równa 5. Wyznacz liczbę  .
.
Do zestawu liczb: 3, 5 i 9 dopisano czwartą liczbę. Mediana otrzymanego w ten sposób zestawu czterech liczb jest większa od mediany początkowego zestawu trzech liczb. Uzasadnij, że dopisana liczba jest większa od 5.
Z zestawu czterech liczb usunięto jedną liczbę i pozostały liczby 4, 6, 9. Mediana otrzymanego w ten sposób zestawu trzech liczb jest mniejsza od mediany początkowego zestawu czterech liczb. Uzasadnij, że usunięta liczba jest większa od 6.
Zapisano trzy różne liczby, których średnia arytmetyczna jest równa 4, oraz dwie inne liczby, których średnia arytmetyczna jest równa 2. Uzasadnij, że średnia arytmetyczna zestawu tych pięciu liczb jest równa 3,2. Zapisz obliczenia.
Zapisano dwie różne liczby, których średnia arytmetyczna jest równa 4, oraz trzy inne liczby, których średnia arytmetyczna jest równa 2. Uzasadnij, że średnia arytmetyczna zestawu tych pięciu liczb jest równa 2,8. Zapisz obliczenia.
Średnia wieku 15 mieszkańców pewnego bloku wynosi 33 lata. Gdy do wolnego mieszkania wprowadził się nowy mieszkaniec, średnia zwiększyła się o 1 rok. Ile lat ma nowy mieszkaniec?
W sklepie budowlanym zakupiono 21 przedmiotów, przy czym średnia cena zakupu tych przedmiotów była równa 53 zł. Gdyby dodatkowo dokupiono miarkę, to średnia cena zakupionych przedmiotów zmalałaby do 51 zł. Jaka jest cena miarki?
Zdarzenie losowe polega na wybraniu jednej krawędzi ustalonego wcześniej graniastosłupa prostego. Oblicz jakie jest prawdopodobieństwo, że wybrana krawędź jest krawędzią boczną tego graniastosłupa.
W każdym z dwóch pudełek znajduje się tyle samo kul. Kule te są w jednym z dwóch kolorów: czarne lub białe. Prawdopodobieństwo wylosowania kuli białej z pierwszego pudełka jest równe 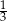 i jest dwa razy większe niż prawdopodobieństwo wylosowania kuli czarnej z drugiego pudełka. Umieszczamy teraz wszystkie kule z tych dwóch pudełek w jednym trzecim pudełku. Jakie jest prawdopodobieństwo wylosowania kuli białej z trzeciego pudełka?
i jest dwa razy większe niż prawdopodobieństwo wylosowania kuli czarnej z drugiego pudełka. Umieszczamy teraz wszystkie kule z tych dwóch pudełek w jednym trzecim pudełku. Jakie jest prawdopodobieństwo wylosowania kuli białej z trzeciego pudełka?
Na diagramie przedstawiono wyniki (w centymetrach) uzyskane przez zawodników uczestniczących w finale konkursu skoku wzwyż.
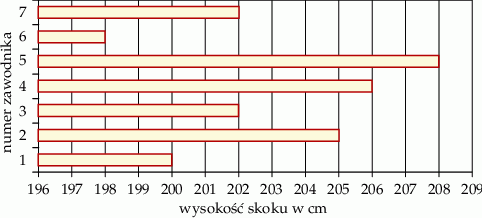
Ilu zawodników uzyskało wynik wyższy od średniej arytmetycznej wyników wszystkich uczestników finału tego konkursu?
A) 2 B) 3 C) 4 D) 5
Na diagramie przedstawiono wzrost (w centymetrach) ośmiu koszykarzy.
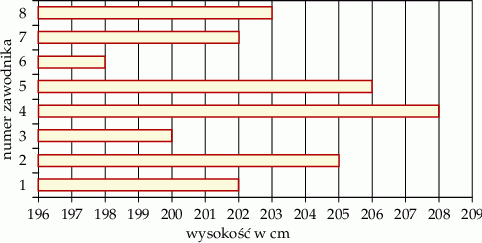
Ilu z tych zawodników ma wzrost mniejszy niż średni wzrost wszystkich zawodników przedstawionych na diagramie?
A) 2 B) 3 C) 4 D) 5
Średnia arytmetyczna dwóch liczb wynosi 20. Jeśli jedną z nich zwiększymy dwukrotnie, a drugą zmniejszymy o 50%, to średnia arytmetyczna zwiększy się o 2. Wyznacz te liczby.
Średnia arytmetyczna dwóch liczb wynosi 16. Jeśli jedną z nich zmniejszymy dwukrotnie, a drugą zwiększymy o 50%, to średnia arytmetyczna zwiększy się o 2. Wyznacz te liczby.
Średnia arytmetyczna liczb 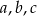 jest równa 15. Oblicz średnią arytmetyczną liczb
jest równa 15. Oblicz średnią arytmetyczną liczb 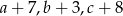 .
.
W pierwszej urnie znajduje się 5 kul białych i 17 kul czarnych. W drugiej urnie znajduje się 16 kul białych i 34 kule czarne. Ile kul białych należy przełożyć z drugiej urny do pierwszej, aby wylosowanie kuli białej z obu urn było jednakowo prawdopodobne?
W pierwszej urnie znajdują się 4 kule białe i 13 kul czarnych. W drugiej urnie znajduje się 17 kul białych i 26 kul czarnych. Ile kul białych należy przełożyć z drugiej urny do pierwszej, aby wylosowanie kuli białej z obu urn było jednakowo prawdopodobne?
Średnia wieku w pewnej grupie studentów jest równa 23 lata. Średnia wieku tych studentów i ich opiekuna jest równa 24 lata. Opiekun ma 39 lat. Oblicz, ilu studentów jest w tej grupie.
Średnia wieku w pewnej grupie uczniów jest równa 14 lat. Średnia wieku tych uczniów i ich opiekuna jest równa 16 lat. Opiekun ma 40 lat. Oblicz, ilu uczniów jest w tej grupie.

